Analyse d’une matrice sur base de polygones prédéfinis
Import des modules
[ ]:
# import _add_path # for debugging purposes only - can be removed in production
try:
from wolfhece import is_enough
if not is_enough('2.2.31'):
raise ImportError("Please update wolfhece to at least version 2.2.31")
except ImportError:
raise ImportError("Please install the required version of wolfhece: pip install wolfhece>=2.2.30")
from wolfhece.analyze_poly import Array_analysis_polygons, Array_analysis_onepolygon
from wolfhece.wolf_array import WolfArray, header_wolf
from wolfhece.PyVertexvectors import vector, zone, Zones, wolfvertex as wv
import matplotlib.pyplot as plt
import numpy as np
Création d’une matrice de variables aléatoires
[2]:
h = header_wolf()
h.set_origin(25, 55) # Set the origin (lower-left) of the array
h.set_resolution(0.5 , 0.5) # Set the resolution of the array
h.shape = (1000, 2000) # Set the shape of the array (cells along x and y axes)
a = WolfArray(srcheader= h)
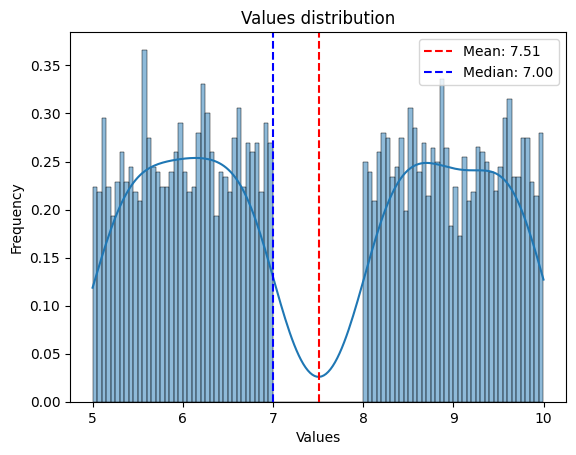
a.array[:,:] = np.random.rand(1000, 2000) * 10
a.mask_lower(5.)
a.set_nullvalue_in_mask()
a.plot_matplotlib(with_legend= True)
print("Number of values in the array:", a.nbnotnull)
Number of values in the array: 1000895
Création de polygones d’analyse
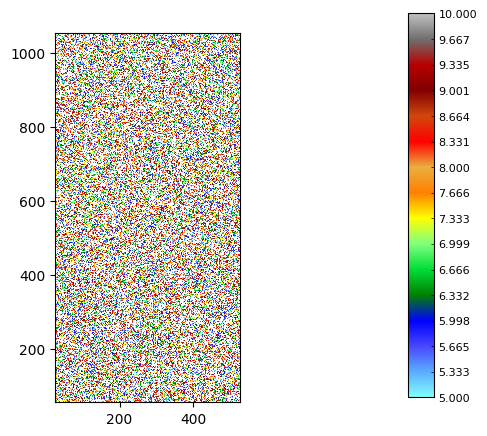
Pour l’exemple, on va définir des polygones réguliers de 50 m x 50 m couvrant toute la matrice.
[3]:
nbx = 1000. * .5 / 50. # Number of polygons along x axis
nby = 2000. * .5 / 50. # Number of polygons along y axis
print(f"Number of polygons along x: {nbx}, y: {nby}")
print(f"Total number of polygons: {nbx * nby}")
# Create polygons
zone_poly = zone(name = 'polygons')
for i in range(int(nbx)):
for j in range(int(nby)):
x = i * 50. + 25. # Offset by the origin
y = j * 50. + 55. # Offset by the origin
poly = vector(name=f'Polygon_{i}_{j}', parentzone=zone_poly)
poly.add_vertices_from_array(np.array([[x, y],
[x + 50, y],
[x + 50, y + 50],
[x, y + 50]]))
poly.force_to_close() # Ensure the polygon is closed
zone_poly.add_vector(poly)
fig, ax = plt.subplots(figsize=(10, 10))
a.plot_matplotlib(figax = (fig, ax))
zone_poly.plot_matplotlib(ax)
ax.set_aspect('equal')
Number of polygons along x: 10.0, y: 20.0
Total number of polygons: 200.0
Création de l’objet d’analyse
[4]:
analyze = Array_analysis_polygons(a, zone_poly)
Analyse des polygones
Comptage du nombre de polygones avec des valeurs strictement positives
Histogramme des valeurs moyennes par polygone
Histogramme des valeurs médianes par polygone
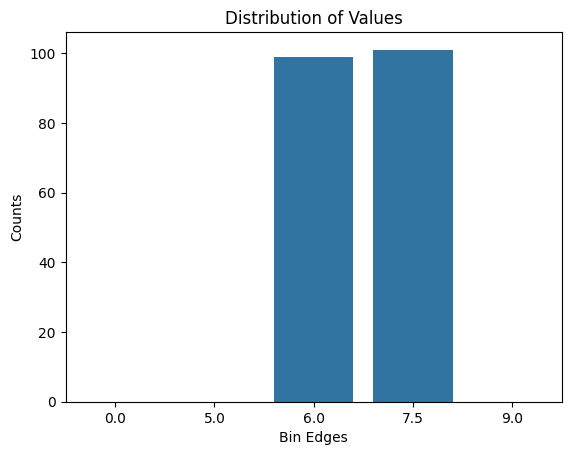
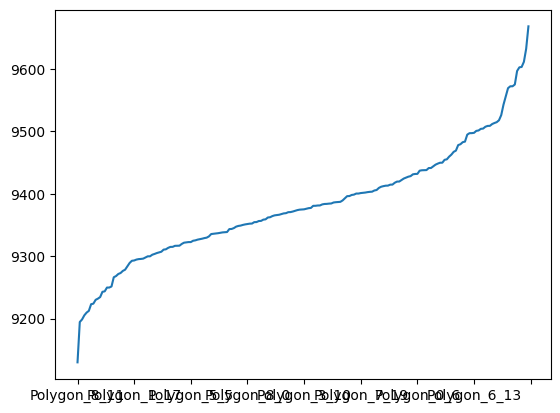
Distribution des volumes par polygone
[5]:
analyze.count_strictly_positive()
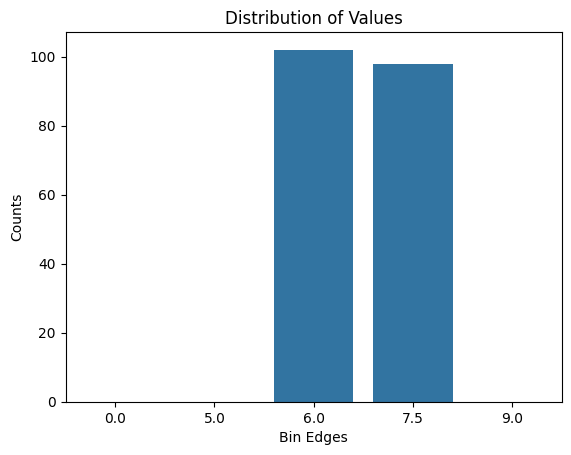
analyze.plot_distributed_values(bins = [0., 5., 6, 7.5, 9., 10.], operator= 'Mean')
analyze.plot_distributed_values(bins = [0., 5., 6, 7.5, 9., 10.], operator= 'Median')
dist = analyze.values('Volume')
dist.sort_values(inplace=True)
dist.plot()
[5]:
<Axes: >
Analyse d’un polygone spécifique
Il est possible de générer un graphique pour chaque polygone.
Au besoin, les clés des polygones peuvent être récupérées avec la propriété keys.
[6]:
analyze.keys
[6]:
['Polygon_0_0',
'Polygon_0_1',
'Polygon_0_2',
'Polygon_0_3',
'Polygon_0_4',
'Polygon_0_5',
'Polygon_0_6',
'Polygon_0_7',
'Polygon_0_8',
'Polygon_0_9',
'Polygon_0_10',
'Polygon_0_11',
'Polygon_0_12',
'Polygon_0_13',
'Polygon_0_14',
'Polygon_0_15',
'Polygon_0_16',
'Polygon_0_17',
'Polygon_0_18',
'Polygon_0_19',
'Polygon_1_0',
'Polygon_1_1',
'Polygon_1_2',
'Polygon_1_3',
'Polygon_1_4',
'Polygon_1_5',
'Polygon_1_6',
'Polygon_1_7',
'Polygon_1_8',
'Polygon_1_9',
'Polygon_1_10',
'Polygon_1_11',
'Polygon_1_12',
'Polygon_1_13',
'Polygon_1_14',
'Polygon_1_15',
'Polygon_1_16',
'Polygon_1_17',
'Polygon_1_18',
'Polygon_1_19',
'Polygon_2_0',
'Polygon_2_1',
'Polygon_2_2',
'Polygon_2_3',
'Polygon_2_4',
'Polygon_2_5',
'Polygon_2_6',
'Polygon_2_7',
'Polygon_2_8',
'Polygon_2_9',
'Polygon_2_10',
'Polygon_2_11',
'Polygon_2_12',
'Polygon_2_13',
'Polygon_2_14',
'Polygon_2_15',
'Polygon_2_16',
'Polygon_2_17',
'Polygon_2_18',
'Polygon_2_19',
'Polygon_3_0',
'Polygon_3_1',
'Polygon_3_2',
'Polygon_3_3',
'Polygon_3_4',
'Polygon_3_5',
'Polygon_3_6',
'Polygon_3_7',
'Polygon_3_8',
'Polygon_3_9',
'Polygon_3_10',
'Polygon_3_11',
'Polygon_3_12',
'Polygon_3_13',
'Polygon_3_14',
'Polygon_3_15',
'Polygon_3_16',
'Polygon_3_17',
'Polygon_3_18',
'Polygon_3_19',
'Polygon_4_0',
'Polygon_4_1',
'Polygon_4_2',
'Polygon_4_3',
'Polygon_4_4',
'Polygon_4_5',
'Polygon_4_6',
'Polygon_4_7',
'Polygon_4_8',
'Polygon_4_9',
'Polygon_4_10',
'Polygon_4_11',
'Polygon_4_12',
'Polygon_4_13',
'Polygon_4_14',
'Polygon_4_15',
'Polygon_4_16',
'Polygon_4_17',
'Polygon_4_18',
'Polygon_4_19',
'Polygon_5_0',
'Polygon_5_1',
'Polygon_5_2',
'Polygon_5_3',
'Polygon_5_4',
'Polygon_5_5',
'Polygon_5_6',
'Polygon_5_7',
'Polygon_5_8',
'Polygon_5_9',
'Polygon_5_10',
'Polygon_5_11',
'Polygon_5_12',
'Polygon_5_13',
'Polygon_5_14',
'Polygon_5_15',
'Polygon_5_16',
'Polygon_5_17',
'Polygon_5_18',
'Polygon_5_19',
'Polygon_6_0',
'Polygon_6_1',
'Polygon_6_2',
'Polygon_6_3',
'Polygon_6_4',
'Polygon_6_5',
'Polygon_6_6',
'Polygon_6_7',
'Polygon_6_8',
'Polygon_6_9',
'Polygon_6_10',
'Polygon_6_11',
'Polygon_6_12',
'Polygon_6_13',
'Polygon_6_14',
'Polygon_6_15',
'Polygon_6_16',
'Polygon_6_17',
'Polygon_6_18',
'Polygon_6_19',
'Polygon_7_0',
'Polygon_7_1',
'Polygon_7_2',
'Polygon_7_3',
'Polygon_7_4',
'Polygon_7_5',
'Polygon_7_6',
'Polygon_7_7',
'Polygon_7_8',
'Polygon_7_9',
'Polygon_7_10',
'Polygon_7_11',
'Polygon_7_12',
'Polygon_7_13',
'Polygon_7_14',
'Polygon_7_15',
'Polygon_7_16',
'Polygon_7_17',
'Polygon_7_18',
'Polygon_7_19',
'Polygon_8_0',
'Polygon_8_1',
'Polygon_8_2',
'Polygon_8_3',
'Polygon_8_4',
'Polygon_8_5',
'Polygon_8_6',
'Polygon_8_7',
'Polygon_8_8',
'Polygon_8_9',
'Polygon_8_10',
'Polygon_8_11',
'Polygon_8_12',
'Polygon_8_13',
'Polygon_8_14',
'Polygon_8_15',
'Polygon_8_16',
'Polygon_8_17',
'Polygon_8_18',
'Polygon_8_19',
'Polygon_9_0',
'Polygon_9_1',
'Polygon_9_2',
'Polygon_9_3',
'Polygon_9_4',
'Polygon_9_5',
'Polygon_9_6',
'Polygon_9_7',
'Polygon_9_8',
'Polygon_9_9',
'Polygon_9_10',
'Polygon_9_11',
'Polygon_9_12',
'Polygon_9_13',
'Polygon_9_14',
'Polygon_9_15',
'Polygon_9_16',
'Polygon_9_17',
'Polygon_9_18',
'Polygon_9_19']
[7]:
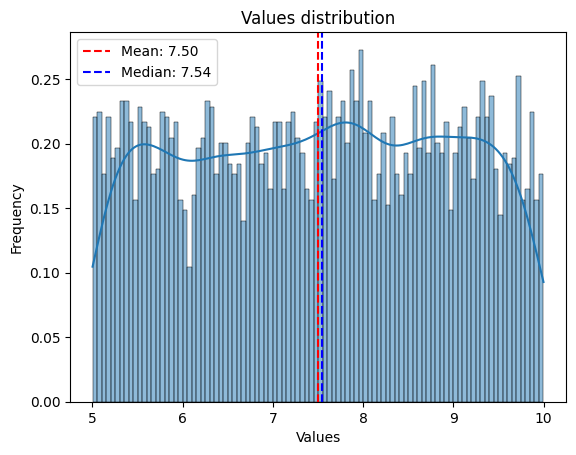
i = 0
j = 0
all_plots = analyze[f'Polygon_{i}_{j}'].plot_values()
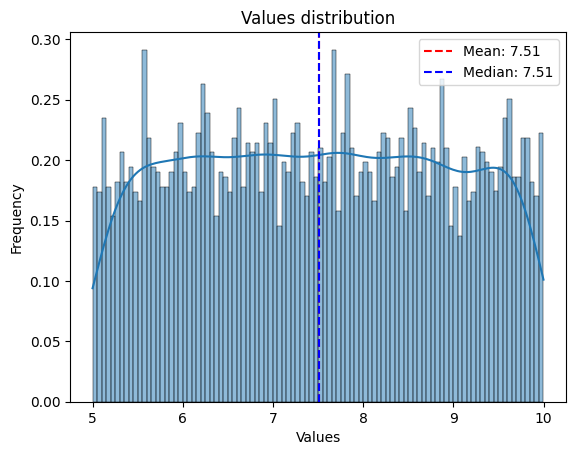
i = 8
j = 15
all_plots = analyze[f'Polygon_{i}_{j}'].plot_values()
Modification des valeurs analysées via le masque de la matrice
Masquage d’une tranche de la matrice et recaclcul des valeurs des polygones.
[8]:
a.array.mask[(a.array > 7.) & (a.array < 8.)] = True
analyze.update_values()
i = 8
j = 15
all_plots = analyze[f'Polygon_{i}_{j}'].plot_values()