Paramètre de Shields

Le paramètre de Shields est un paramètre hydro-sédimentaire.

Il est défini par la formule suivante :

\[\theta = \frac{\tau}{\tau_c}\]

où :

\(\theta\) est le paramètre de Shields,
\(\tau\) est la contrainte de cisaillement exercée par l’eau sur le lit du cours d’eau,
\(\tau_c\) est la contrainte de cisaillement critique, c’est-à-dire la contrainte de cisaillement minimale nécessaire pour initier le mouvement des sédiments.

Le paramètre de Shields est utilisé pour évaluer la stabilité des sédiments dans un cours d’eau. Il permet de déterminer si les conditions hydrauliques sont suffisantes pour entraîner le mouvement des particules sédimentaires. Un \(\theta\) supérieur à 1 indique que les conditions sont suffisantes pour entraîner le mouvement des sédiments, tandis qu’un \(\theta\) inférieur à 1 indique que les conditions ne sont pas suffisantes.

Le diagramme de Shields

Le diagramme de Shields est un graphique qui représente le paramètre de Shields en fonction du nombre de Reynolds et du nombre de Froude. Il est utilisé pour visualiser les conditions hydrauliques dans un cours d’eau et pour évaluer la stabilité des sédiments.

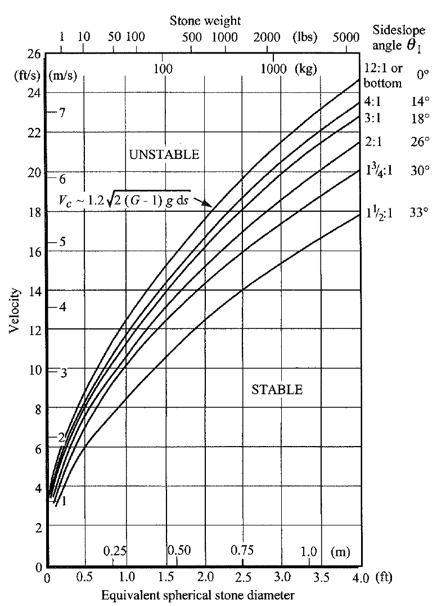
alt text

source : Van Rijn (1984), Sediment Transport, Part I: Bed Load Transport, Journal of Hydraulic Engineering, ASCE, 110(10):1431-1456.

Implémentation en Python

Dans le paquet wolfhece, des outils sont disponibles via le module pyshields pour calculer le paramètre de Shields et tracer le diagramme de Shields sous différentes formes.

## Références

Quelques références utiles pour approfondir le sujet :

Telemac-Mascaret
Yalin, Ferraira da Silva (2001), Fluvial Processes, IAHR Monograph
Fredsoe, Jorgen and Deigaard Rolf. (1992). Mechanics of Coastal Sediment. Sediment Transport. Advanced Series on Ocean Engineering - Vol. 3. World Scientific. Singapure.
Madsen, Ole S., Wood, William. (2002). Sediment Transport Outside the Surf Zone. In: Vincent, L., and Demirbilek, Z. (editors), Coastal Engineering Manual, Part III, Combined wave and current bottom boundary layer flow, Chapter III-6, Engineer Manual 1110-2-1100, U.S. Army Corps of Engineers, Washington, DC.
Nielsen, Peter. (1992). Coastal Bottom Boundary Layers and Sediment Transport. Advanced Series on Ocean Engineering - Vol. 4. World Scientific. Singapure.

Import des modules

[1]:

# import _add_path # for debugging purposes only - remove in production
try:
    required_version = '2.2.30'
    from wolfhece import is_enough
    is_enough(required_version)

    import timeit
    import matplotlib.pyplot as plt

    from wolfhece.pyshields import RHO_SEAWATER, RHO_PUREWATER, RHO_SEDIMENT, get_shields_cr, get_d_cr
    from wolfhece.pyshields import shieldsdia_dim, shieldsdia_dstar, shieldsdia_sadim # routines graphiques
    from wolfhece.pyshields import get_d_cr_susp, get_transport_mode # suspension
except ImportError as e:
    print(f"Import error: {e}")
    print("Please ensure that the wolfhece package is installed and up to date.")
    print(f"Minimal version required: {required_version}")

Shields critique

Différentes formulations existent :

Le paramètre which permet de choisir la fonction via son index dans la liste [(get_sadim,get_psi_cr),(get_dstar,get_psi_cr2),(get_dstar,get_psi_cr3)]

which = 0 -> (get_sadim,get_psi_cr) - reference
which = 1 -> (get_dstar,get_psi_cr2) - reference
which = 2 (défaut) -> (get_dstar,get_psi_cr3) - reference Fluvial Processes, IAHR 2001, pp 6-9

[3]:

print("Default formula  is which == 2 (get_dstar, get_psi_cr3)\n")
for which in [0, 1, 2]:
    res = get_shields_cr(d = 0.2e-3, rho = RHO_PUREWATER, which=which)
    print(f"Result for which = {which}")
    # critical_shear_velocity, tau_cr, xadim_val, psicr
    print(f"Critical shear velocity: {res[0]:.4f} m/s, Tau_cr: {res[1]:.4f} N/m², Xadim_val: {res[2]:.4f}, Psi_cr: {res[3]:.4f}\n")

Default formula  is which == 2 (get_dstar, get_psi_cr3)

Result for which = 0
Critical shear velocity: 0.0128 m/s, Tau_cr: 0.1649 N/m², Xadim_val: 2.8449, Psi_cr: 0.0509

Result for which = 1
Critical shear velocity: 0.0127 m/s, Tau_cr: 0.1606 N/m², Xadim_val: 5.0592, Psi_cr: 0.0496

Result for which = 2
Critical shear velocity: 0.0139 m/s, Tau_cr: 0.1942 N/m², Xadim_val: 5.0592, Psi_cr: 0.0600

Graphiques

Il est possible de tracer le diagramme de Shields sous différentes formes :

shieldsdia_dstar : le paramètre de Shields en fonction du paramètre d’échelle de Shields (dstar) - axes adimensionnés
shieldsdia_sadim : le paramètre de Shields en fonction du paramètre sadim - axes adimensionnés
shieldsdia_dim : le paramètre de Shields en fonction du diamètre hydraulique - axes dimensionnés

Les arguments s_psicr et dstar_psicr permettent de tracer un point spécifique sur le diagramme. Ils sont des tuples de la forme (valeur, psicr) où valeur est la valeur du paramètre à tracer et psicr est la valeur critique du paramètre.

[4]:

fig, ax = plt.subplots(3,1)

s = RHO_SEDIMENT / RHO_PUREWATER # ratio of sediment density to water density
shear_cr, tau_cr, xadim, psi_cr =  get_shields_cr(d = 0.2e-3, rho = RHO_PUREWATER, which = 2)

shieldsdia_sadim(s_psicr=(s,psi_cr), figax=(fig,ax[0]))
shieldsdia_dstar(s_psicr=(s,psi_cr), figax=(fig,ax[1]))
shieldsdia_dim(figax=(fig,ax[2]))

ax[0].set_title('Modified Shields diagram')
fig.set_size_inches(10,10)
fig.tight_layout()
fig.show()

C:\Users\pierre\AppData\Local\Temp\ipykernel_12488\4240051310.py:13: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
  fig.show()

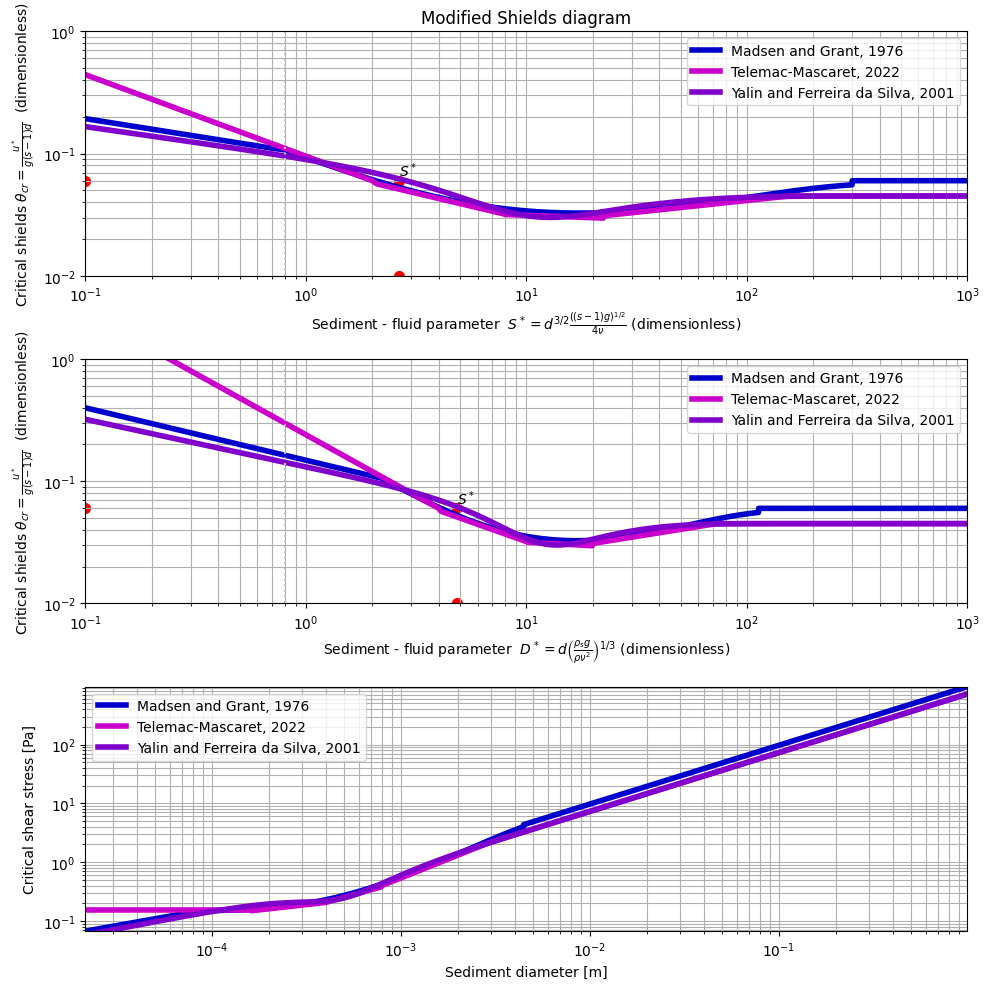
Détermination du paramètre critique sur base du diamètre des sédiments

Dans cette logique, la formule est explicite. Cela ne pose pas de difficulté particulière.

Détermination du diamètre critique des sédiments sur base de la tension de cisaillement

Dans cette logique, la formule est implicite. Il faut donc utiliser une méthode numérique pour trouver le diamètre critique des sédiments.

Ceci est implémenté dans la fonction get_d_cr qui utilise la méthode brenth par défaut pour trouver la racine. Elle fournit en plus le diamètre au sens de la formule d’Izbach/Izbash/Isbach

alt text

source

Exemple de calcul avec Manning-Strickler

[5]:

dcr_shields, dcr_izbach = get_d_cr(q = 10.,
                                   h = 2.,
                                   K = 25.)

print(f"Critical diameter (Shields): {dcr_shields:.4f} m, Critical diameter (Izbach): {dcr_izbach:.4f} m")

Critical diameter (Shields): 0.4276 m, Critical diameter (Izbach): 0.5363 m

Exemple avec Colebrook-White

Il est possible de calculer le diamètre critique des sédiments en fonction de la contrainte de cisaillement et d’une hauteur de rugosité à utiliser dans la formule de Colebrook-White.

[6]:

dcr_shields, dcr_izbach = get_d_cr(q = 10.,
                                   h = 2.,
                                   K = 0.05,
                                   friction_law='Colebrook')

print(f"Critical diameter (Shields): {dcr_shields:.4f} m, Critical diameter (Izbach): {dcr_izbach:.4f} m")

Critical diameter (Shields): 0.1396 m, Critical diameter (Izbach): 0.5363 m

Mise en suspension et mode de transport

Il est également possible de calculer :

le diamètre critique d’emportement par suspension à 50%
le mode de transport des sédiments

Note : actuellement seule la formule de Manning-Strickler est implémentée mais l’extension est aisée

[7]:

dsusp = get_d_cr_susp(q = 10.,
                      h = 2.,
                      K = 25.,
                      rhom = RHO_SEDIMENT,
                      rho = RHO_PUREWATER)

print(f"Critical diameter for suspension: {dsusp:.4f} m")

Critical diameter for suspension: 0.0152 m

[8]:

from wolfhece.pyshields import BED_LOAD, SUSPENDED_LOAD_100, SUSPENDED_LOAD_50, WASH_LOAD

mode = get_transport_mode(d = 0.2e-3,
                          q = 10.,
                          h = 2.,
                          K = 25.,
                          rhom = RHO_SEDIMENT,
                          rho = RHO_PUREWATER)

if mode == BED_LOAD:
    print("Bed load transport")
elif mode == SUSPENDED_LOAD_100:
    print("Suspended load transport at 100%")
elif mode == SUSPENDED_LOAD_50:
    print("Suspended load transport at 50%")
elif mode == WASH_LOAD:
    print("Wash load transport")

Wash load transport