WOLF Hydro

Warning

Cette version de la documentation date de janvier 2022 et ne tient pas compte des derniers développements.

La mise à jour se fera progressivement.

WOLFHydro est la composante hydrologique du logiciel de résolution d’équations hydrauliques et hydrologiques de la suite WOLF. Ce module WOLFHydro est composé d’un code principal programmé en Orienté Objet en Fortran 2003 et d’un code Python3 de post-traitement.

Même si WOLF dispose d’outils de calcul hydrologiques à base physique (ruissellement de surface selon une hypothèse d’one diffusive ou une approche complète, écoulement souterrain non saturé en colonnes 1D et totalement 3D en saturé), l’accent sera principalement placé ici sur les modèles plus conceptuels qu’ils soient globaux, semi-distribués ou maillés.

Le code de calcul principal en Fortran contient toutes les fonctionnalités de prétraitement des données, d’optimisation et d’application des modèles hydrologiques sur un bassin versant. Ces procédures, les plus chronophages, seront ainsi menées à bien par un outil offrant une rapidité et une puissance de calcul scientifique incontesté.

Le code Python offre, quant à lui, toutes les procédures automatiques de regroupement, d’affichage et de traitement des résultats. Il est également capable de lire des cartes matricielles et/ou vectorielles sorties par WOLFHydro et il permet de générer au moyen d’une interface graphique les différents fichiers de paramètres permettant de lancer le code Fortran de WOLF. Ses procédures et son organisation gardent la même structure que le code Fortran permettant une forte compatibilité et une bonne communication entre les deux langages, notamment au moyen de librairies compilées via « f2py » et l’appel direct de DLL.

Définition de l’entité de calcul

Bassin versant (quasi-)naturel

Données topographiques/altimétriques

La donnée de base est une information topographique matricielle. WOLFHydro permet de gérer nativement les formats :

• WOLF binaire

• GeoTiff

• Float ESRI (.flt)

Tout autre format matriciel supporté par la librairie GDAL peut également être importé facilement.

En Wallonie, le système de projection par défaut est Lambert72 (EPSG :31370) et le référentiel altimétrique DNG (Deuxième Nivellement Général). En région frontalière, la combinaison d’informations de référentiels distincts est aisée grâce à l’exploitation de l’outil GDAL.

Le modèle numérique de terrain disponible sur l’ensemble du territoire de la Région wallonne « Lidar 2013-2014 » peut par exemple être aggloméré à la taille de la maille désirée via un opérateur mathématique à choisir parmi trois possibilités : min, max, mean. Les données de base à la résolution de 1 m sont agglomérées par défaut grâce à une moyenne arithmétique pour des résolution de : 10, 20, 100, 250, 500 et 5000 mètres. Cela facilite la mise en place de nouvelles modélisations pour des résolutions typiques.

La zone à étudier doit être définie par l’utilisateur au moyen des bornes Xmin, Xmax, Ymin, Ymax dans le système de projection courant. Un découpage sera réalisé automatiquement sur cette base afin de réduire le nombre d’éléments à considérer dans les procédures suivantes.

Masque de calcul

Dans l’emprise rectangulaire définie par le modèle numérique de terrain, il est possible de définir un masque de calcul. Ce masque est représenté par une matrice binaire (extension « .nap ») en réel simple précision où une valeur unitaire désigne une maille de calcul et une valeur nulle une maille à ne pas considérer.

Ce masque permet d’extraire du calcul hydrologique une zone ou plusieurs zones spécifiques (exemple : zone de carrière en terrain imperméable et pour laquelle la communication au réseau hydrographique est uniquement gérée par pompage).

Corrections hydrologiques du MNT

Par défaut, WOLFHydro se base sur l’hypothèse que la direction de l’écoulement de surface à chaque maille est régie par la plus grande pente. Il est donc essentiel que chaque maille possède au moins une maille voisine d’altitude inférieure. Cette hypothèse permet de s’assurer que toutes les mailles du domaine potentiel de calcul contribuent à la transmission de pluie vers l’exutoire.

L’algorithme D8 est régulièrement utilisé en hydrologie, mais WOLF dispose de ses propres procédures internes qui étendent les capacités du D8 de façon à le rendre compatible avec une potentielle discrétisation spatiale au sens des volumes finis. Cette fonctionnalité est utile si le ruissellement de surface devait être calculé grâce à l’un des modules de calcul 2D à base physique. Ainsi, le nombre de voisins à considérer dans la recherche de la plus grande pente est laissé libre, en croix (4 voisins), mailles de contour (8 voisins). Ce choix est laissé à l’utilisateur sur base du modèle utilisé in fine.

La séparation de mailles en écoulement de ruissellement et de rivière est ensuite opérée sur base d’un seuil d’accumulation paramétré [km²].

Néanmoins, pour arriver à ce résultat, il est indispensable de corriger les matrices de topographies de façon à s’assurer que chaque maille dispose d’une pente strictement positive (définition conventionnelle). Il existe différentes façons de corriger une zone de plat et de dépression [2] :

• La première consiste à remplir la zone de dépression en élevant l’altitude des mailles concernées et former une zone de plat. Cette zone de plat sera elle-même corrigée par la suite de façon à diriger celles-ci vers l’élément d’altitude la plus faible adjacent à cette zone et possédant un voisin d’altitude inférieure.

• Une autre méthode consiste à choisir automatiquement entre le remplissage précédent ou la création d’une brèche.

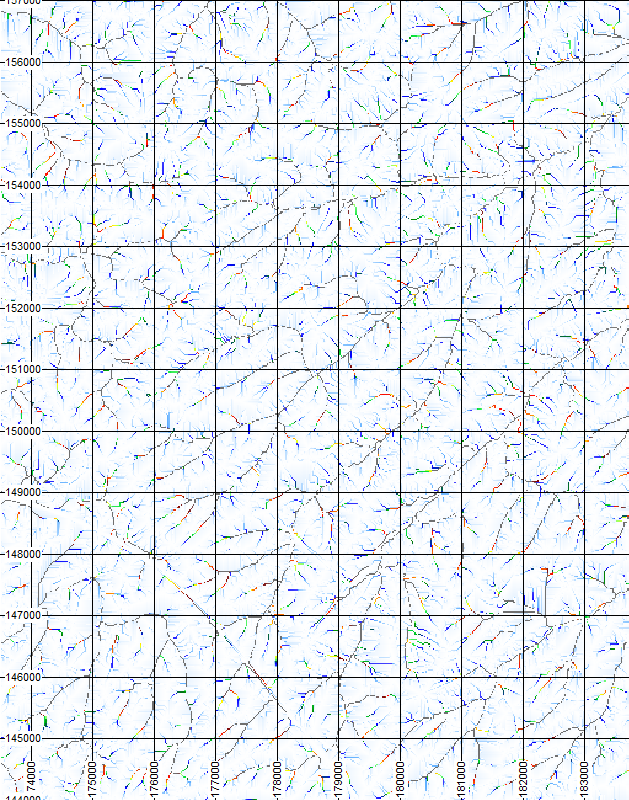
1. Topographie corrigée

2. Carte de différences entre la topographie corrigée et la topographie initiale

Figure 1 Correction de topographie appliquée sur le bassin versant de l’Orbais

Echanges forcés

Il est également possible de définir dans le code des « échanges forcés ». Un échange forcé est défini comme étant un lien direct entre deux mailles. Dans ce cas, l’élément amont de la paire d’échange forcé transférera toujours ses flux à l’élément aval de cette même paire. Le principe de plus grande pente ne sera donc pas appliqué à toute maille amont de cette paire, rendant cet élément indépendant de la topographie.

Ces échanges forcés permettront de prendre en compte des flux passant en dessous de certains reliefs, constructions humaines ou encore des écoulements souterrains. Lors de l’utilisation d’un maillage de plus en plus dense, une série de nouveaux obstacles peuvent apparaître et créer davantage de zones de dépression à corriger.

Par exemple, un ruisseau passant sous une autoroute, un pont ou, pire encore, un viaduc aura un impact significatif sur une correction à l’aveugle de topographie. En effet, l’obstacle possédant une altitude plus élevée, le dernier élément du ruisseau en amont de celui-ci ne trouvera pas de voisin avec une altitude plus basse et formera ainsi une zone de dépression. Celle-ci pouvant être très grande en fonction de l’altitude de l’obstacle. Selon la méthode de correction choisie, la zone de dépression sera remplie pour atteindre la même altitude que l’obstacle ou l’obstacle sera creusé de façon à lier les deux extrémités du ruisseau. Dans les deux cas, une grande perte d’information est générée. Dans le premier, la correction topographique peut être extrêmement importante (un viaduc par exemple) et déformer sur une grande surface les reliefs des mailles amont et les transformer en zones de plat. Dans le deuxième cas, la suppression de l’obstacle pourrait également effacer un réseau d’écoulement, par exemple, l’écoulement le long d’une autoroute alors que la surface drainée par celle-ci n’est pas toujours négligeable. L’interruption de la voirie forcerait une partie de sa surface à s’écouler à cet endroit et pourrait provoquer un apport local de débit non souhaité.

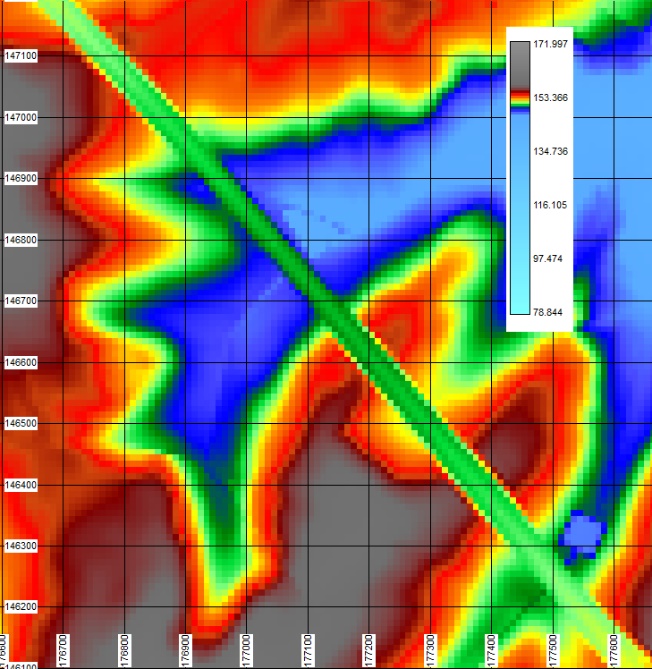
Un lien direct entre les mailles rivière de part et d’autre de l’obstacle permet de conserver davantage la topographie originale du bassin et ainsi perdre moins d’information. Un exemple d’application de ces échanges forcés est représenté sur les Figure 2, Figure 3 et Figure 1. La Figure 2 représente une portion du bassin versant de l’Orbais (résolution de 10 m x 10 m) dans laquelle, le ruisseau passe en dessous de l’autoroute. L’algorithme de correction de topographie se basant sur les éléments de plus grandes pentes, ne pourra pas détecter le cours d’eau passe sous l’autoroute et modifiera, de ce fait, la topographie, comme représenté sur Figure 3. Il est possible d’observer qu’une grande partie de la surface en amont de l’autoroute est fortement déformée (remplissage d’environ 4 mètres) et transformée en une zone presque plate. En appliquant, des échanges forcés sur le ruisseau de part et autre de l’autoroute, on garde, de ce fait, une topographie quasiment identique à la configuration initiale. La configuration réelle de l’écoulement est donc conservée.

Deux types d’échanges forcés sont définis :

• Des échanges forcés « rivières » : la distance entre les deux éléments d’une paire sera évaluée par le biais d’une distance euclidienne. Cette distance sera utilisée dans l’évaluation de la pente et du temps de transfert entre les deux mailles de la paire. Ce type d’échange forcé est recommandé pour franchir des obstacles ou représenter un écoulement souterrain. Dès lors, il est parfaitement adapté pour représenter l’exemple de l’Orbais, mentionné ci-dessus

• Des échanges forcés « réservoirs » : les deux éléments d’une paire seront considérés comme voisins, et la distance les séparant sera donc la taille d’une maille. Ce type d’échange forcé est particulièrement utile pour représenter des étendues d’eau, des réservoirs ou des lacs.

Figure 2 Carte MNT initiale à 10 m x 10 m aux alentours du bassin d’orage n°5 de l’Orbais à proximité de l’autoroute (vert). Les points rouges sont les échanges forcés à appliquer à cette topographie.

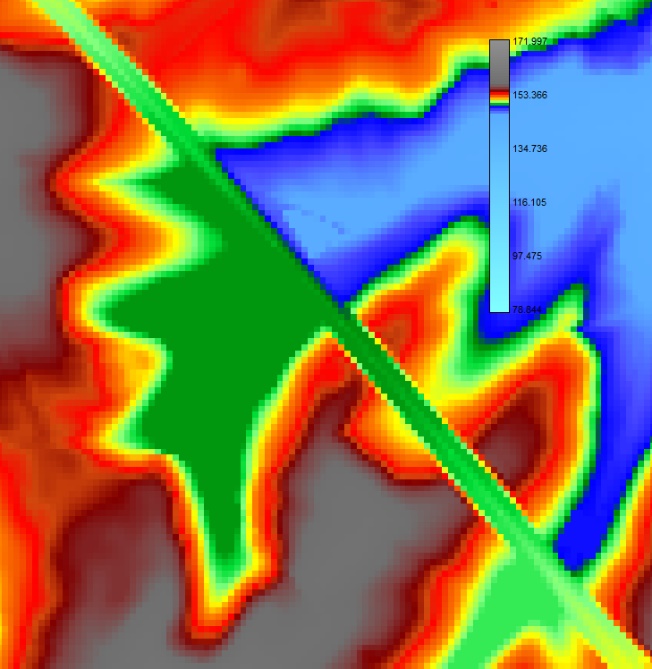
Figure 3 Carte de topographie corrigée sans échanges forcés aux alentours du bassin d’orage n°5 de l’Orbais à proximité de l’autoroute

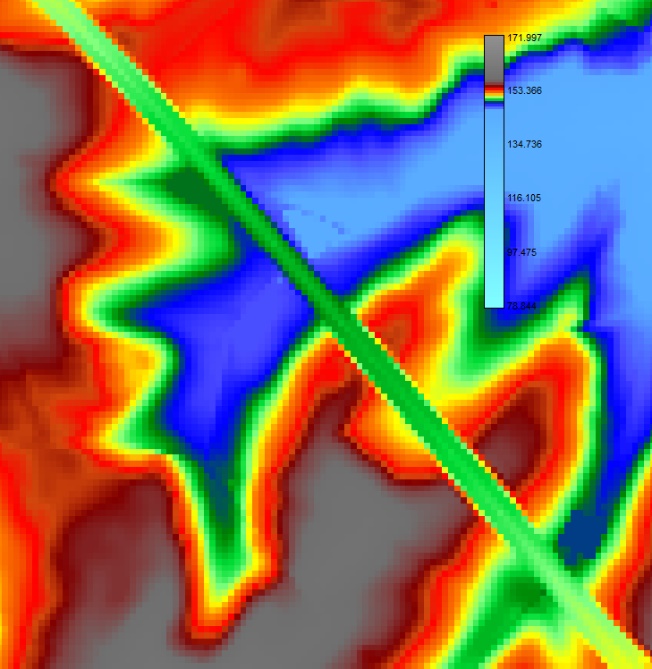
Figure 4 Carte de topographie corrigée avec échanges forcés aux alentours du bassin d’orage n°5 de l’Orbais à proximité de l’autoroute

Recherche de l’élément de plus grande pente

A ce stade, chaque maille devrait soit disposer d’une connexion par échange forcé avec une maille aval, soit au moins un voisin avec une altitude plus faible. Toutes les mailles sont parcourues afin de déterminer son voisin de plus grande pente auquel le flux sera transmis. En utilisant cette méthode, une connexion est créée entre la maille amont et sa maille aval. Un réseau de mailles est ainsi créé dans lequel plusieurs mailles amont peuvent être connectées à une maille aval, mais une seule maille aval est connectée à une maille amont.

Dans le code, ces connexions sont maintenues en mémoire sous la forme de pointeurs.

Cependant, lorsqu’un modèle d’onde diffusive est choisi comme modèle de surface, les flux de ruissellement dépendront de la pente de surface libre instantanée. Dans ce cas, un flux pourra être dirigé vers plusieurs mailles en fonction des conditions locales transitoires.

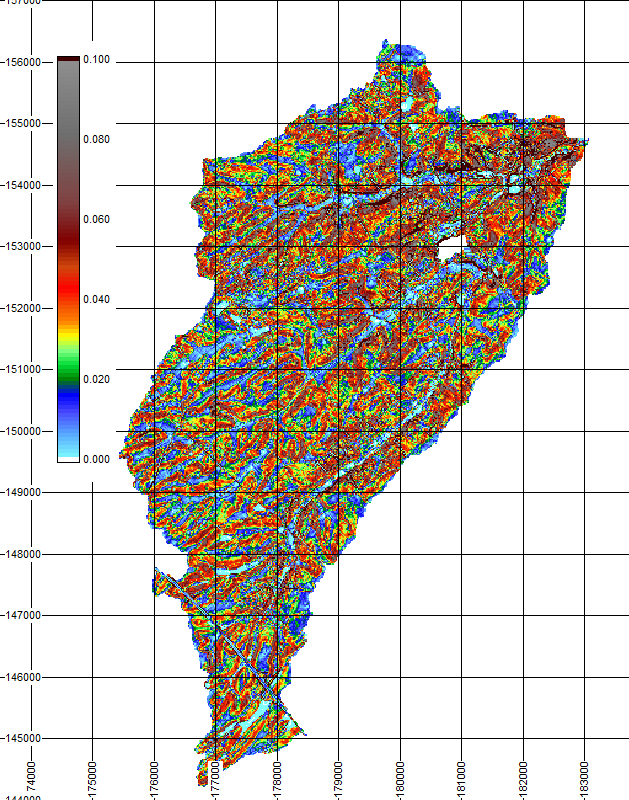
Figure 5 Normes des pentes locales sur le bassin versant de l’Orbais et calculées avec

\[\begin{split}\\sqrt {{{\\left( {\\frac{{\\partial z}}{{\\partial x}}} \\right)}^2} + {{\\left( {\\frac{{\\partial z}}{{\\partial y}}} \\right)}^2}}\end{split}\]

Pour rappel, il est possible de définir dans WOLF une matrice de masque qui permet d’exclure certaines régions du domaine. Dans la Figure 5, de tels éléments sont affichés par une zone blanche qui est présente au milieu de la carte. Elle peut représenter, par exemple ici, une carrière qui capte toute l’eau environnante sans la restituer vers l’exutoire. En effet, tout débit échangé avec une maille masquée ne se retrouvera pas à l’exutoire.

Accumulation et formation du réseau hydrographique

Afin de déterminer quels éléments dans le domaine représenteront les rivières, la notion de convergence/accumulation est utilisée. La convergence/l’accumulation est définie comme étant la surface totale drainée en ce point (la somme des surfaces des mailles amont).

Dans le code WOLFHydro , il y a trois types de mailles :

• La maille « rivière » : elle est censée représenter, dans la réalité, les ruisseaux, rivières et fleuves. Elle est définie comme étant une maille possédant une accumulation supérieure à un certain seuil, paramètre fourni par l’utilisateur.

• La maille « masquée » : est une maille qui a été exclue du domaine par l’utilisateur.

• La maille « bassin versant » est une maille qui n’est pas « rivière » et dans le domaine.

Figure 6 Matrice des convergences sur le bassin versant de l’Orbais

Dans le cas particulier d’un échange forcé, les deux éléments de la paire doivent absolument être des mailles rivières et seront considérés comme tels.

Détermination du bassin versant topographique

Pour identifier le bassin versant associé à l’exutoire demandé, toutes les mailles seront une nouvelle fois parcourues, en partant des éléments avec l’altitude la plus basse vers les plus hautes. Tous les éléments échangeant directement ou indirectement un flux avec l’exutoire seront compris dans le bassin. Une liste de ces mailles sera sauvée dans un fichier mais également conservé en mémoire lors du calcul. Les autres éléments ne seront plus pris en compte dans la suite des procédures et seront rejetés du domaine d’étude.

Préparation du bassin versant

Division du bassin versant en sous-bassins (optionnel)

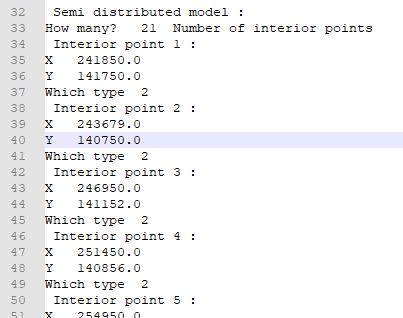
Il est possible de diviser le bassin versant total en plusieurs sous-bassins par le biais d’une définition de « points intérieurs ». Ceux-ci deviendront les exutoires de chaque sous-bassin. L’utilité d’une telle division est multiple :

• Evaluer les débits à plusieurs points intermédiaires dans le bassin et ainsi mieux analyser l’évolution des débits le long du réseau hydrographique ;

• Comparer directement les débits simulés avec ceux mesurés à des stations de mesure ;

• Tenir compte de structures anthropiques telles que des barrages, des bassins d’orages… Les surfaces de bassin influencées par cette structure peuvent ainsi être isolées et traitées de façon spécifique afin de reproduire individuellement leurs fonctionnements (code de post-traitement Python) ;

• Permettre des simulations semi-distribuées de différentes structures de modèles hydrologiques.

Attribution d’une occupation du sol à chaque maille

Pour un modèle spatialement distribué, deux types de cartes d’occupation du sol peuvent être lues :

• Carte d’occupation du sol de Wallonie vectorielle (COSW) ;

• Carte CORINE d’occupation du sol matricielle du projet européen Copernicus (résolution de 100m x 100 m).

Sur base de l’emprise spatiale du domaine de calcul, une première étape de sélection de la zone strictement utile est opérée. Cela permet de répéter par la suite des opérations de prétraitement sans alourdir le calcul avec des données sur une emprise potentiellement inutile. Ces opérations de « cropping » sont réalisées via des commandes GDAL.

D’autres cartes peuvent également être importées pour autant que leur format soit de type ESRI « .shp » ou « .flt » et qu’un fichier texte de conversion des codifications d’occupation du sol vers les classes disponibles dans WOLF soit fourni.

Actuellement, WOLF considère 6 grandes catégories d’occupation du sol :

1. Forêts

2. Prairies

3. Cultures

4. Urbain

5. Eau

6. Rivières

Cette vision assez classique permet entre autres une compatibilité du modèle avec l’approche ADALI utilisée historiquement en Province du Brabant Wallon.

Une maille de calcul retient le pourcentage d’occupations de sol pour chaque classe. Si des données vectorielles sont utilisées, les surfaces partielles sont calculées par croisement géométrique des polygones avec l’emprise de la maille. Cette procédure d’attribution des occupations du sol pouvant être très coûteuse en temps, les résultats du calcul sont sauvés sous la forme de fichiers matriciels indépendants afin de pouvoir être relus plus rapidement lors du redémarrage du calcul.

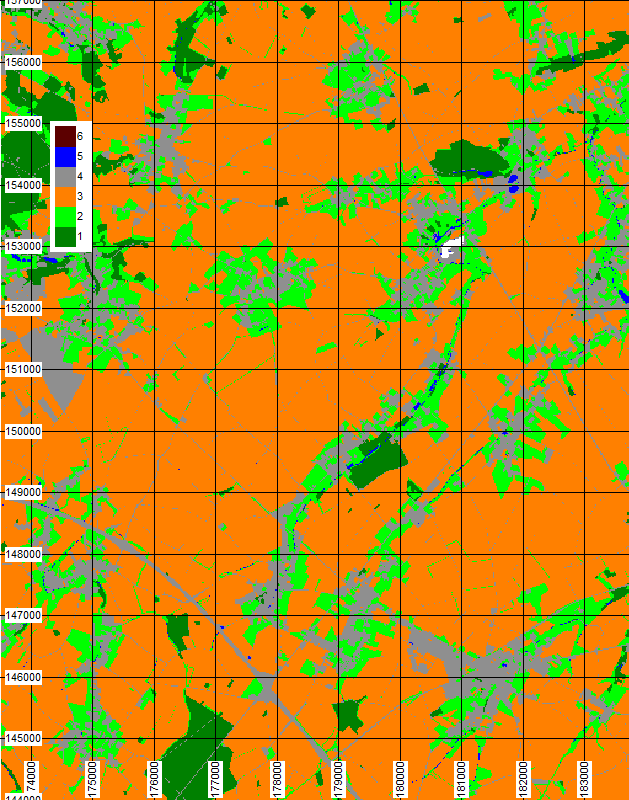
Figure 7 Occupations majoritaires du sol d’après des cartes COSW sur le bassin versant de l’Orbais Les numérotations des occupations du sol correspondent à celles présentées dans le chapitre.

Les données écrites dans la carte Figure 7 représentent uniquement l’occupation dominante au sein d’une maille.

Estimation des temps de ruissellement entre mailles (isochrones)

Trois méthodes différentes coexistent actuellement pour estimer la vitesse d’écoulement et finalement le temps de transfert des flux entre les mailles.

• La première se base sur les coefficients fixés par le projet Adali et dépend des occupations du sol et des pentes en chaque maille ;

• La deuxième exploite les vitesses de transfert de la référence Applied Hydrology [1988, Ven Te Chow] et dépend également des occupations du sol et des pentes en chaque maille ;

• La troisième se base sur le nombre de Froude et ne dépend que des pentes locales. Dans cette méthode, une distinction est également effectuée entre les mailles « rivières » et les mailles « bassin versant ».

Ces méthodes sont expliquées plus en détail dans les sections correspondantes.

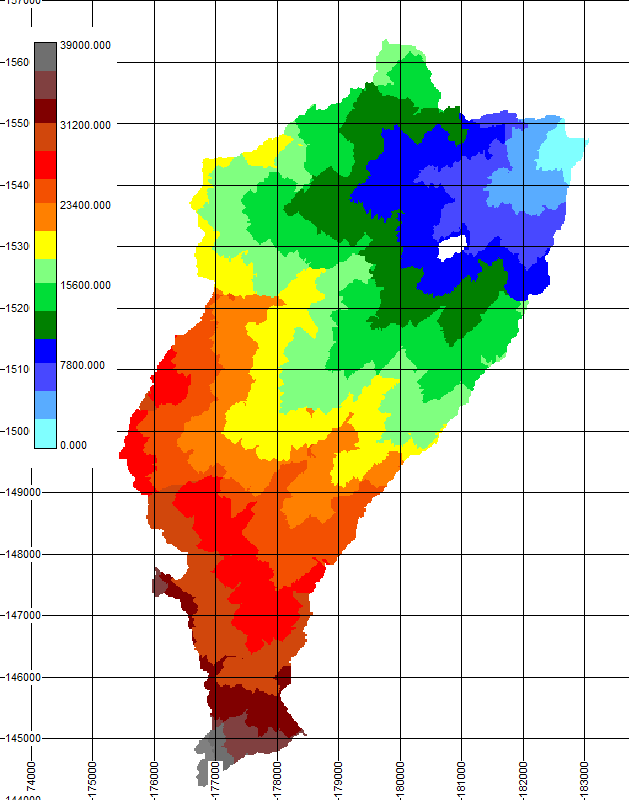
Figure 8 Temps de propagation jusque l’exutoire en secondes

Estimation des coefficients de ruissellement

Dans une modélisation événementielle spatialisée, les coefficients de ruissellement représentent la portion de pluie tombée sur une maille qui sera transmise à l’exutoire. Cette valeur dépend a priori du type de sol et de l’occupation du sol. En effet, des zones de végétations denses ralentiront davantage l’écoulement favorisant ainsi l’infiltration de l’eau de pluie dans le sol. Par opposition, les milieux urbains et champs agricoles empêchent beaucoup plus l’infiltration et, en l’absence d’obstacles, favorisent le ruissellement.

Il existe différentes lois pour déterminer la portion de pluie ruisselée ou, de façon complémentaire, le coefficient d’infiltration. Mais une approche simple consiste à utiliser un tableau à double entrée dont les coefficients ne dépendent que de l’occupation du sol et de la pente. Un exemple de valeurs pour ces coefficients de ruissellement est fourni par la méthode Adali qui sera détaillée dans la Section 0.

Pour appliquer ce coefficient de ruissellement, plusieurs hypothèses peuvent être posées par le modélisateur :

• Dans un modèle à couche de surface unique, les quantités infiltrées sont considérées comme étant perdues. Dès lors, la crue à l’exutoire est uniquement liée au ruissellement de surface ;

• Dans un modèle à couches multiples, les quantités infiltrées peuvent participer à la crue avec une dynamique propre ;

• La portion de débit ruisselé dépend uniquement du type de sol et de la pente locale ;

• Les valeurs de ces coefficients peuvent être déterminés par l’utilisateur dans un fichier annexe ;

• Les coefficients de ruissellement sont constants ou évolutifs en fonction du temps ou dépendent encore de pluies antérieures.

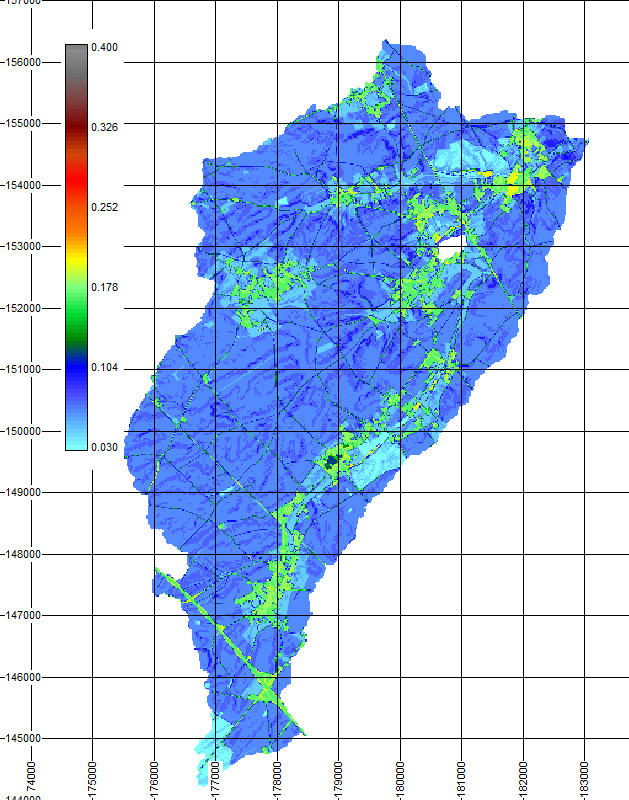
Figure 9 Coefficients de ruissellement pour le bassin versant de l’Orbais

Construction des hydrogrammes unitaires (approche linéaire)

Grâce aux temps de propagation déterminés dans la Section 2.2.3, il est possible de construire des hydrogrammes unitaires de chaque sous-bassin, voire de chaque maille rivière afin d’alimenter un modèle hydraulique de façon totalement distribuée. Les hydrogrammes unitaires sont construits grâce aux isochrones calées sur le pas de temps de calcul. Par conséquent, le nombre d’isochrones sera lié à ce pas de temps et l’hydrogramme sera d’autant plus lisse si ce nombre est grand.

Une fois cette répartition opérée, il est possible de déterminer les débits en tout point du filaire et à l’exutoire (local ou global) en tenant compte d’une fonction de production (coefficient de ruissellement ou autre).

Réseau de voies hydrauliques

La différence fondamentale entre un bassin versant (quasi-)naturel et un réseau de voies hydrauliques est la présence d’organes de régulation (barrages mobiles, écluses, centrales hydroélectriques, passe à poissons…) qui influent sur la gestion des masses d’eau.

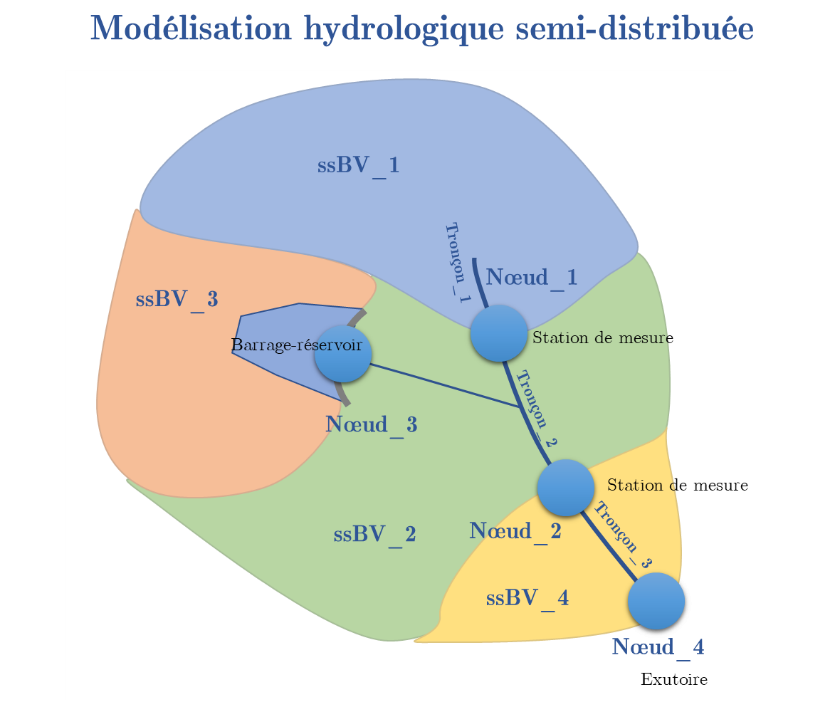
Figure 10 Bassin versant quasi-naturel modélisé par une approche semi-distribuée

Ainsi, la modélisation conceptuelle d’un réseau au sein de WOLFHydro consiste en une décomposition de celui-ci en deux éléments distincts :

• Les nœuds

• Les tronçons

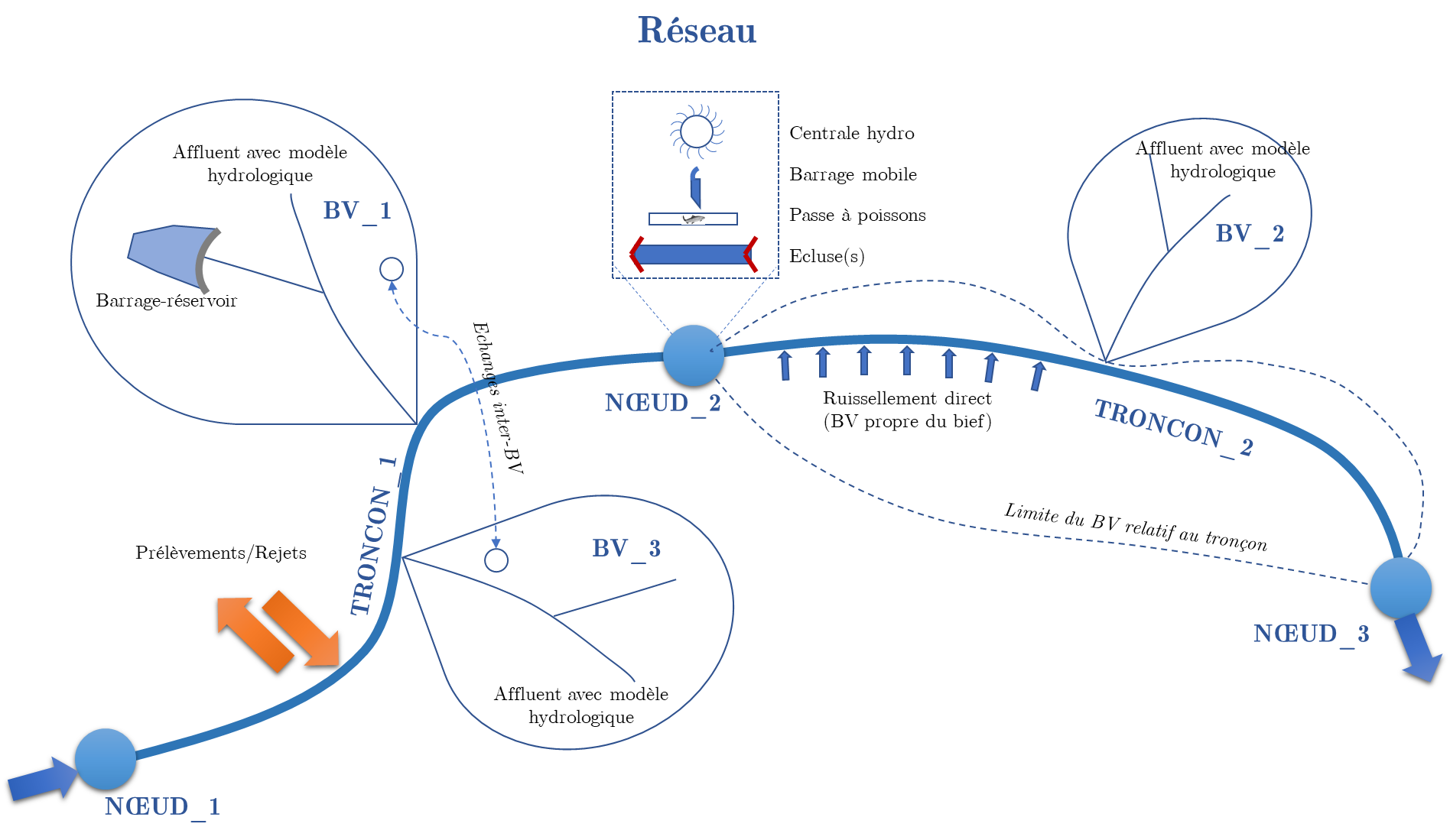
Figure 11 Réseau de voies hydrauliques d’un fleuve

Nœud

La variable principale d’un nœud est un flux d’échange entre deux tronçons. Typiquement, pour un bassin versant, des nœuds seront positionnés au droit des stations de mesure et le flux sera le débit local. Pour un réseau, ce flux peut être la résultante de plusieurs contributions liées aux éléments classiquement trouvés à cet endroit :

• Un barrage mobile

• Une ou plusieurs écluses

• Une centrale hydroélectrique

• Une passe à poissons

• Des pertes

Ces éléments ne sont pas nécessairement exhaustifs mais tous doivent faire l’objet d’un paramétrage permettant d’évaluer les flux au pas de temps retenu.

Tronçon

La variable principale d’un tronçon est un volume avec des variables dérivées potentielles si une relation explicite hauteur/volume/surface est fournie.

Un tronçon fait donc un bilan volumique de son contenu sur base de plusieurs flux d’échanges :

• Les flux aux nœuds ;

• Les apports des affluents qui sont individuellement modélisés ;

• Les apports directs de la fraction du bassin versant contenue entre deux nœuds dont on a soustrait les surfaces correspondantes au point précédent ;

• Des prélèvements et/ou rejets ponctuels identifiés et pour lesquels une caractérisation quantitative peut être faite au pas de temps retenu.

Détermination de la topologie et modèle de calcul

Des procédures similaires à l’analyse d’un bassin versant naturel doivent permettre de définir une première topologie de réseau sur base uniquement d’un modèle numérique de terrain duquel auront été préalablement masquées les mailles faisant partie des modèles hydrologiques locaux.

L’utilisation « d’échanges forcés » permettront de répondre à des spécificités locales pour lesquelles la topographie de surface ne permet pas de représenter correctement la réalité de terrain.

Les nœuds du réseau seront définis comme « points intérieurs », cf. 2.2.1. De cette manière, les sous-bassins obtenus permettront d’évaluer les apports directs par un modèle à paramétrer.

Le bilan de masse pour chaque pas de temps sera finalement résolu en post-traitement Python.

Réseau complexe

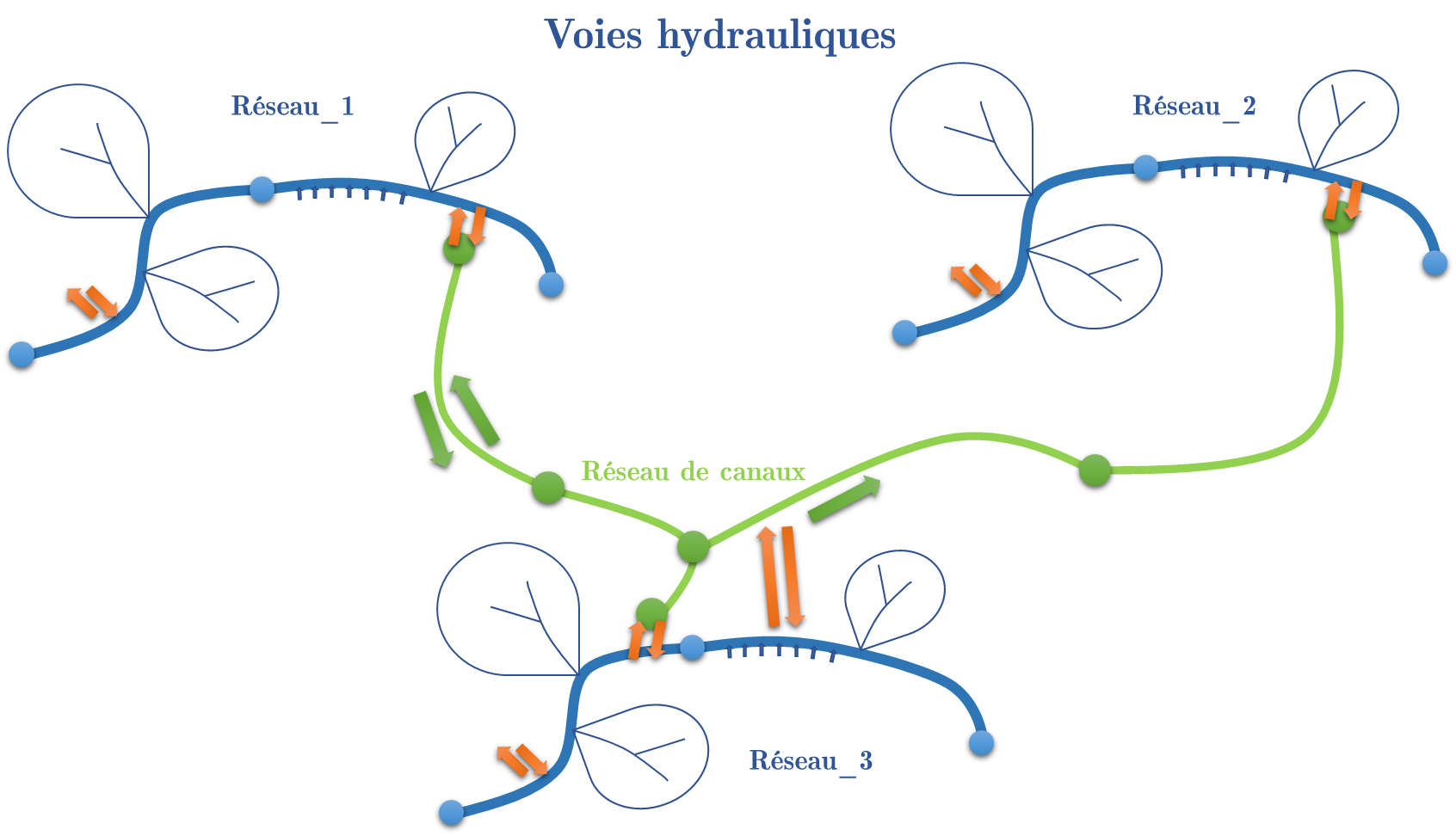
Au-delà du réseau de voies hydrauliques, limité au bassin versant d’un seul fleuve, il est également possible d’ajouter un niveau de complexité supplémentaire en reliant les réseaux de plusieurs fleuves via un réseau de canaux artificiels.

Figure 12 Réseau complexe de voies hydrauliques de plusieurs fleuves reliés par des canaux artificiels

Dans ce cas, les échanges via les canaux sont des flux supplémentaires à évaluer et à attacher soit à des nœuds ou à des tronçons spécifiques d’un sous-modèle. Le réseau de canaux est également modélisé sur la base d’un ensemble de nœuds/tronçons. La différence principale avec un réseau de voies hydrauliques tel que défini précédemment est l’absence de bassin versant propre et donc l’impossibilité de déterminer sa topologie sur base d’une analyse topographique.

Cette topologie de réseau doit obligatoirement résulter d’une analyse spécifique et imposée manuellement en exploitant les objets Python à disposition.

Description des modèles hydrologiques

Structure générale

La philosophie derrière le squelette du modèle proposé est de bâtir une suite de « modules » qui est suffisamment flexible pour y appliquer une grande partie des modèles déjà existants et bien connus en hydrologie, mais aussi de permettre toute sorte de modifications simples. L’objectif final est de comparer de façon aisée les forces et les inconvénients lié à la structure du modèle.

Il existe trois types de modules :

• Module de production : caractérisé par une architecture pouvant contenir plusieurs entrées et fournir plusieurs sorties. Il calcule une fonction d’état qui détermine comment un flux peut être décomposé et partagé parmi les autres modules.

• Module de transfert : caractérisé par une seule entrée (lumped) ou une matrice (gridded) et apte à fournir une seule sortie. Cette étape traite le flux d’une manière dépendant de la signification physique attribuée à ce module. Elle influencera donc principalement la variabilité temporelle des débits soumis à cette procédure. Plusieurs équations différentielles peuvent être appliquées, mais il est également possible d’appliquer un hydrogramme unitaire (HU) ou une fonction de transfert de type réservoir linéaire.

• Module de bilan : caractérisé par plusieurs entrées, mais apte à fournir seulement une sortie. Son utilité se démarque dans le regroupement de plusieurs résultats provenant d’autres modules. Il contient également la manière dont ces résultats doivent être combinés pour que le résultat final soit aussi proche que possible des observations ou données intermédiaires.

Un modèle complet est une combinaison d’un ou de plusieurs modules aussi bien en série qu’en parallèle. En général, plusieurs données seront fournies en entrée de ce groupe ou combinaison de modules, telles que la pluie ou l’évapotranspiration. L’objectif final sera très souvent d’obtenir, à la fin, au moins une sortie qui représentera le débit à l’exutoire du bassin versant. Si cependant plusieurs sorties sont présentes, les autres représenteront dès lors des pertes. L’évapotranspiration effective ou encore des échanges souterrains peuvent être des exemples de ce type de pertes.

Modèles disponibles

Modèles 0D - Lumped

Les modèles globaux, dit « lumped » en anglais, identifient l’hydrosystème comme une entité unique. Ils sont principalement définis par la position de l’exutoire et la surface drainée. Dans ce type de modèle, on fait l’hypothèse que la variabilité spatiale du bassin versant ne joue pas un rôle prédominant et que seules des caractéristiques globales influencent les débits évalués à l’exutoire. Ces caractéristiques propres à chaque bassin seront représentées par des paramètres. Ceux-ci peuvent avoir une signification physique ou être purement conceptuels, définis de manière à garder une flexibilité suffisante et, par ce biais, être capables de caractériser un maximum de bassins. Ce type de modèle n’est, par conséquent, pas adapté à l’analyse d’impact d’un aménagement local.

Réservoir linéaire

Il est très fréquent en hydrologie de modéliser un bassin à l’aide d’un réservoir linéaire. Ce modèle composé d’un seul module de transfert prend en entrée les pluies effectives et sort les débits estimés.

L’équation qui en résulte est donnée par

\[K\;\frac{{dy}}{{dt}} = x - y\],

avec \K\ la constante de récession qui représente la diminution constante du débit de base en fonction du temps. Les variables $x$ et \y\ représentent respectivement les débits entrant et sortant dans le réservoir.

La réponse unitaire analytique \h(t)\ d’une telle équation est bien connue et prend la forme de l’exponentielle décroissante suivante

\[h(t) = \frac{1}{K}\;\exp ( - t/K)\].

La solution générale, quant à elle, est donnée par l’expression ci-dessous

\[y(t) = y({t_0})\;\exp \left( {\frac{{{t_0} - t}}{K}} \right) + \int_{{t_0}}^t {\frac{{x(\tau )}}{K}\;\exp \left( { - \frac{{t - \tau }}{K}} \right)\;d\tau } \].

Modèle de Nash

Modéliser un bassin versant avec uniquement un réservoir est cependant trop simpliste et ne permet généralement pas de représenter correctement toute la complexité de certains bassins versants et la grande variabilité de ceux-ci.

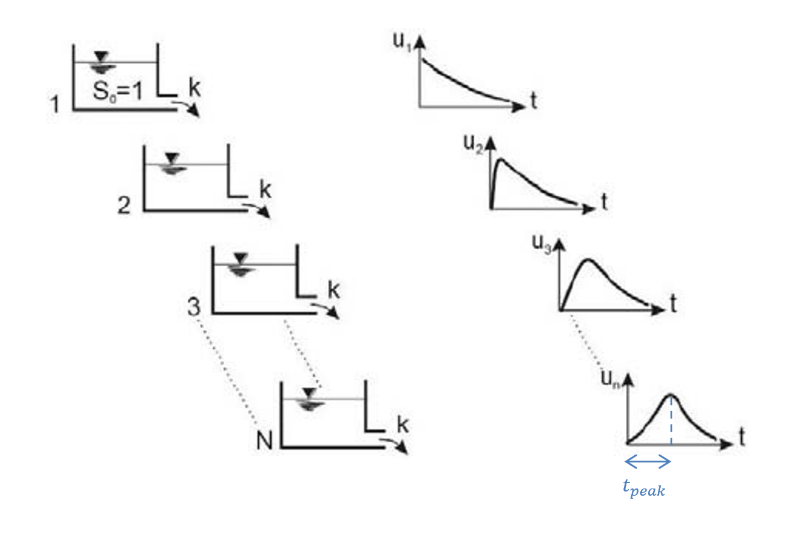
C’est dans cette optique que le modèle de Nash fut introduit [1]. Il propose de ne pas considérer qu’un seul réservoir linéaire, mais une combinaison de réservoirs linéaires identiques disposés en série. Les constantes de récession $K$ de chaque bassin sont dès lors les mêmes.

Ce modèle comprend deux paramètres : un paramètre $K$ pour représenter le temps de récession de chaque réservoir ; et un nouveau paramètre $n$ qui caractérise le nombre de réservoir à considérer. A l’instar du réservoir linéaire, ce modèle est toujours composé d’un seul module.

Figure 13 Nash model

Le débit unitaire \{u_n}\ à la sortie du \{n^{{\rm{i\`e me}}}}\ réservoir est donné par la formule analytique suivante

\[{u_n}(t) = \frac{1}{{K{\mkern 1mu} \Gamma (n)}}{\left( {\frac{t}{K}} \right)^{n - 1}}\exp \left( {\frac{{ - t}}{K}} \right)\]

avec \Gamma la fonction Gamma définie comme

Le pic de cet hydrogramme unitaire survient au temps ${t_{{\rm{peak}}}}$

\[{t_{{\rm{peak}}}} = K\;(n - 1)\]

et le débit de pointe à ce temps est donné par

\[{q_p} = \frac{1}{{K\;\Gamma (n)}}\;{(n - 1)^{(n - 1)}}\;\exp (1 - n)\]

Grâce à l’équation , il existe un lien direct entre la constante $K$ et le temps auquel le pic est souhaité. Cette dernière est nettement plus intuitive et possède un sens physique très clair. C’est pour cette raison que ${t_{{\rm{peak}}}}$ sera le paramètre à prendre en entrée avec le $n$, le nombre de réservoir, dans le fichier paramètre du modèle.

Modèle VHM

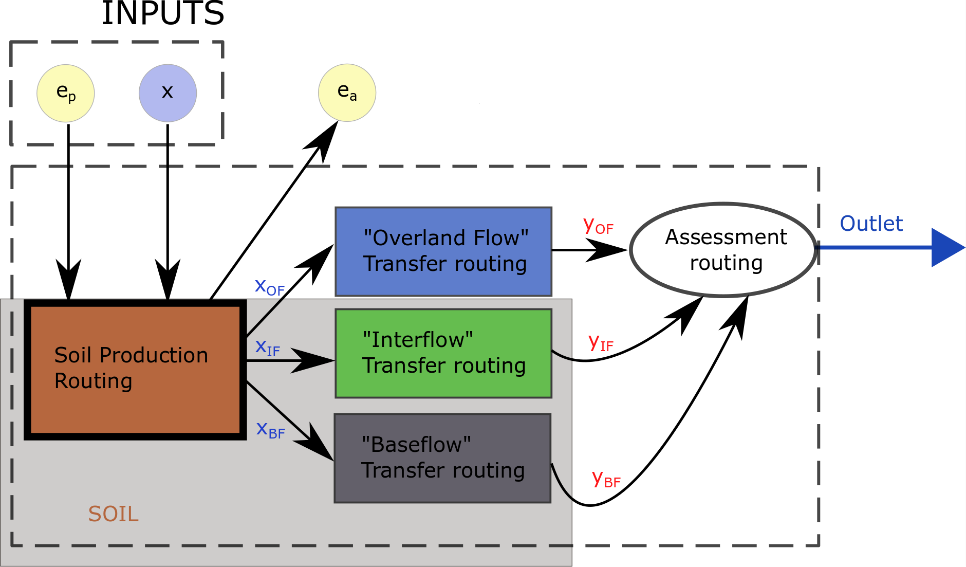
Le modèle VHM introduit par P. Willems [2] possède 12 paramètres. Ce modèle conceptuel fait l’hypothèse que le flux est décomposé en trois composantes à échelles de temps différentes :

• Un débit très rapide censé représenter l’écoulement par ruissellement ou « overland flow »,

• Un débit rapide censé représenter l’écoulement de subsurface ou « interflow »

• Un débit lent censé représenter l’écoulement souterrain ou le comportement des nappes phréatiques. C’est le débit de base ou « baseflow ».

La décomposition de ces flux se fait grâce à une fonction de production utilisant une technique de filtre numérique digital se basant sur une méthode de filtre de Chapman [3] généralisée. P.Willems pointe la grande similitude entre ce filtre et l’équation d’un modèle prenant en compte un réservoir linéaire. Cependant, dans la méthode initiale, la répartition entre les débits rapides et lents aurait été égalitaire. C’est pourquoi P. Willems a généralisé la méthode en introduisant un paramètre supplémentaire permettant de contrôler la fraction des débits distribués entre les couches.

Figure 14 Structure du modèle VHMl

En reprenant la vision générale par modules, ce modèle peut être décomposé de la manière suivante :

• 1 module de productionCe module contient une équation représentant l’état du sol $u$.

Celui-ci est modélisé comme un réservoir linéaire rempli par une fraction de pluie ${x_u}$ auquel on soustrait l’évapotranspiration réelle ${e_a}$. Ces deux éléments sont eux-mêmes fonction du niveau relatif de remplissage du réservoir \u/{u_{{\rm{max}}}}\. Il est possible d’appliquer deux formes de fonction pour déterminer \{x_u}\  en fonction de x : une loi exponentielle ou une loi linéaire. Ce choix est laissé à l’utilisateur.

\[\frac{du}{dt} = x_{u} - e_{a}\]

\[\begin{split}x_{u} = f_{u}.x\ \left\{ \begin{array}{r} f_{u} = a_{u1} - e^{a_{u2}\left( \frac{u}{u_{\max}} \right)^{a_{u3}}} \\ f_{u} = a_{u1} + a_{u2}\frac{u}{u_{\max}}\ \ \ \ \ \ \ \ \end{array} \right.\\end{split}\]

\[e_{a} = \frac{u}{u_{evap}}e_{p} \leq e_{p}\]

Les trois fractions de pluie sont déterminées par la méthode de filtre de Chapman généralisée, avec, ${x_{OF}}$, la portion d’eau ruisselée, ${x_{IF}}$ la portion d’eau attribuée à l’écoulement intermédiaire et ${x_{BF}}$ la portion restante à attribuer à l’écoulement de base. Les équations à appliquer sont les suivantes :

\[\begin{split}x_{IF} = f_{IF}.x\ \left\{ \begin{array}{r} f_{IF} = e^{a_{IF1} + a_{IF2}\left( \frac{u}{u_{\max}} \right)}\ \ \ \ \ \ \ \ \ \ \\ f_{IF} = e^{a_{IF1} + a_{IF2}\left( \frac{u}{u_{\max}} \right)}s^{a_{IF3}} \end{array} \right.\\end{split}\]

\[\begin{split}x_{OF} = f_{OF}.x\ \left\{ \begin{array}{r} f_{OF} = e^{a_{OF1} + a_{OF2}\left( \frac{u}{u_{\max}} \right)}\ \ \ \ \ \ \ \ \ \ \\ f_{OF} = e^{a_{OF1} + a_{OF2}\left( \frac{u}{u_{\max}} \right)}s^{a_{OF3}} \end{array} \right.\\end{split}\]

\[x_{BF} = x - \left( x_{u} + x_{OF} + x_{IF} \right)\]

• 3 modules de transfert qui sont ici des réservoirs linéairesLes trois différentes couches d’écoulement sont représentées par des réservoirs linéaires acceptant en entrée les portions de pluie qui leurs sont attribuées. Les débits sortant de ces réservoirs auront tous les trois des temps caractéristiques d’ordre de grandeur différents et modélisés par les constantes de récession ${k_{OF}}$, ${k_{IF}}$ et ${k_{BF}}$.

\[k_{OF}\frac{dy_{OF}}{dt} = x_{OF} - y_{OF}\]

\[k_{IF}\frac{dy_{IF}}{dt} = x_{IF} - y_{IF}\]

\[k_{BF}\frac{dy_{BF}}{dt} = x_{BF} - y_{BF}\]

Ces équations différentielles ont été résolues dans WOLFHydro sous leurs formes discrètes. L’utilisateur a le choix de les résoudre numériquement à l’aide d’un schéma explicite ou implicite. Une méthode de Runge-Kutta (R-K) est également utilisée et l’ordre de cette méthode peut également être choisi par l’utilisateur.

• 1 module de bilanFinalement, on considère que de débit mesuré à l’exutoire est fourni par la somme directe des trois écoulements.

\[Outlet = y_{OF} + y_{IF} + y_{BF}\]

Modèles GR4H/GR4J

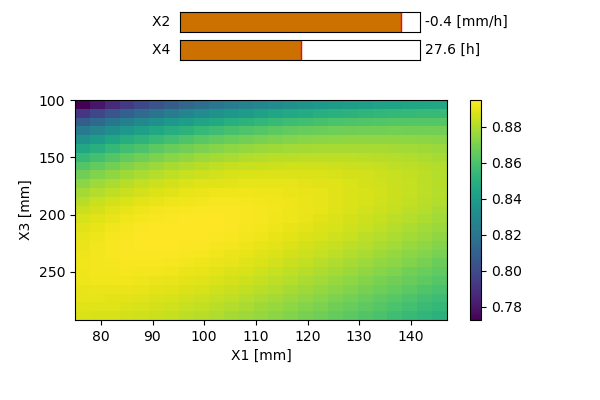
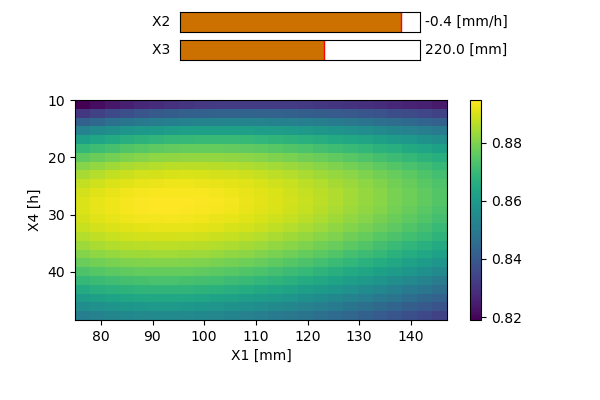
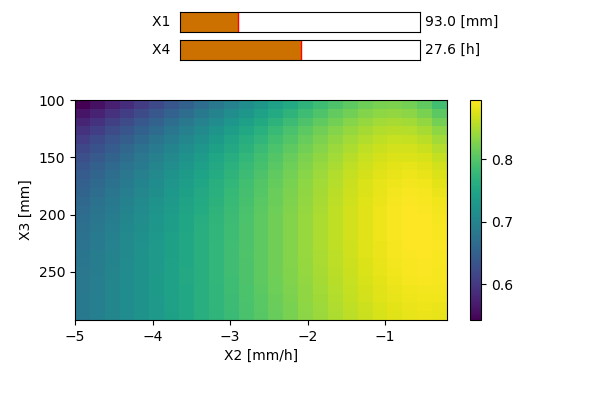
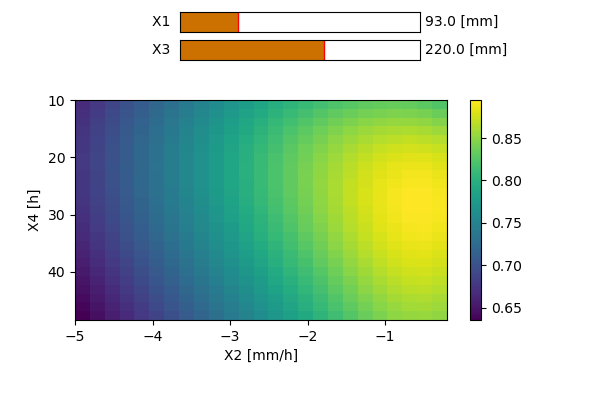
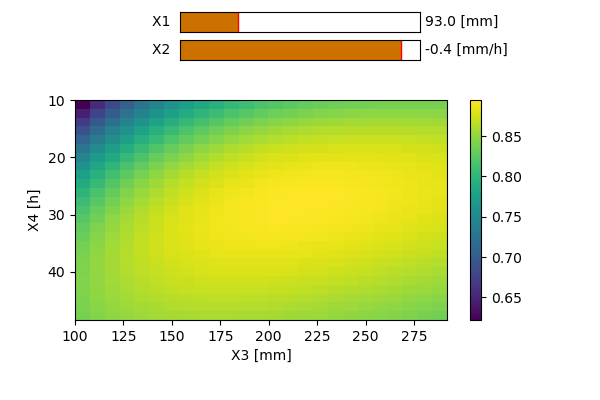
Les modèles GR4J [4] et GR4H [5] (modèle de Génie Rural à 4 paramètres Journalier/Horaire) sont tous les deux des modèles dits « lumped » et conceptuels à 4 paramètres. Comme leurs noms l’indiquent le premier modèle est surtout adapté pour des simulations à pas journalier, tandis que le second est conçu pour réaliser des simulations à pas horaire.

Les paramètres du modèle sont :

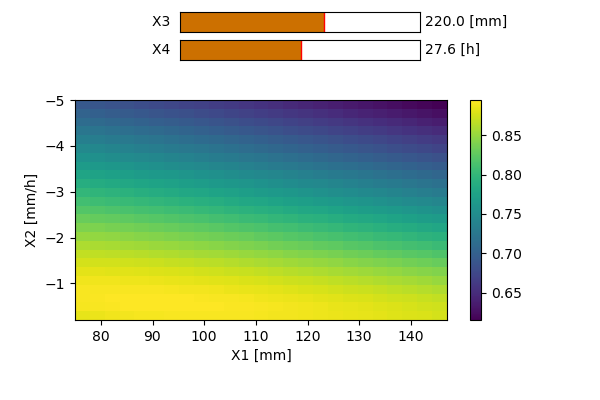
• X1 [mm] : La capacité du réservoir de production du sol

• X2 [mm] : Influence uniquement les pertes ou gains en eau dans le bassin versant. Si le signe est positif, on parlera d’apport ; si le signe est négatif, on parlera d’export. Ce phénomène peut être induit par des échanges entre les nappes phréatiques d’autres bassins voisins. Certaines pertes peuvent également s’expliquer par d’éventuels transferts d’eau vers des couches plus profondes du sol.

• X3 [mm] : La capacité du réservoir de routage.

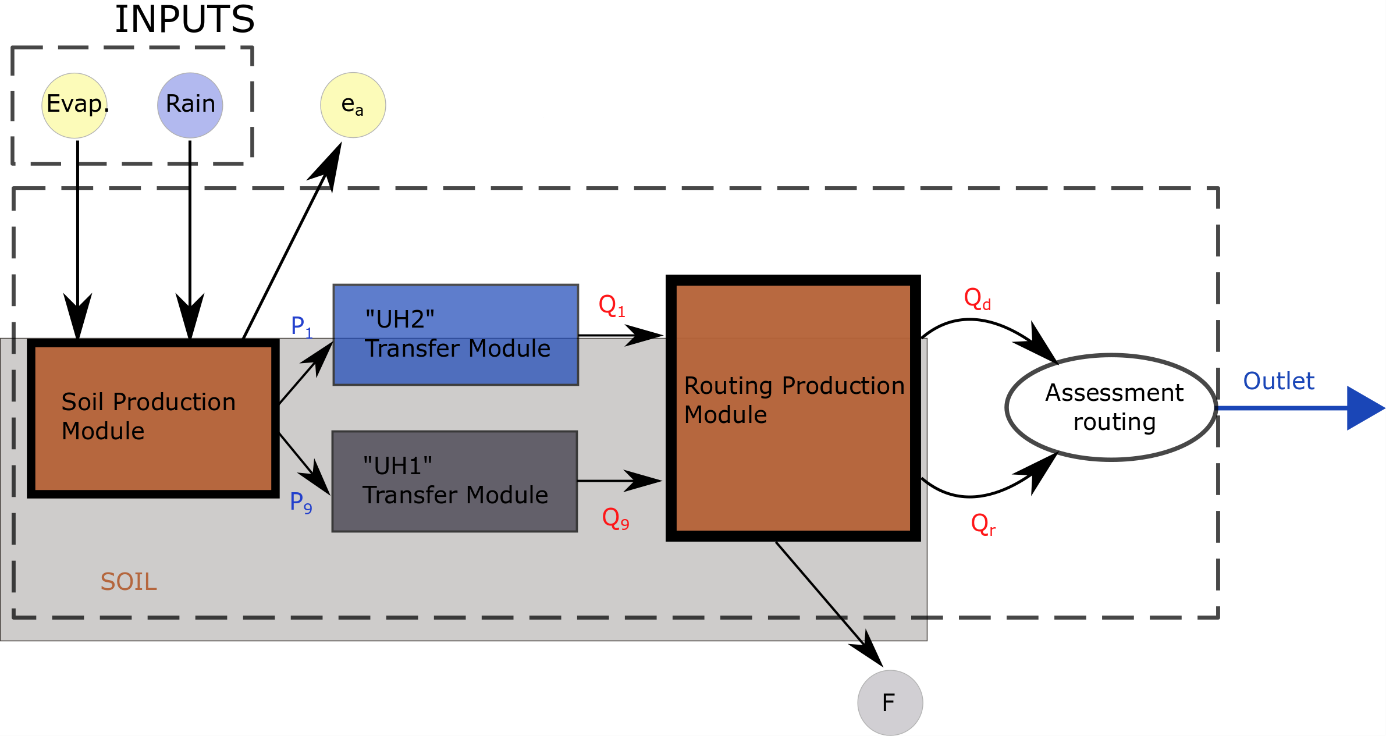
• X4 [heures ou jours] : Le temps caractéristique permettant de former les hydrogrammes unitaires dans les modules de transfert.La structure des deux modèles est équivalente et celle-ci est représentée sur la Figure 151512. Les seules différences entre ceux-ci résident dans la valeur de certains coefficients.

Figure 15 Structure des modèles GR4H/GR4J

Ce modèle n’est pas intrinsèquement conservatif. Des pertes surviennent à cause d’évapotranspiration, mais également à cause d’échanges souterrains notés $F$ entre bassins versants ou la présence de nappe phréatiques communes à plusieurs bassins versants.

Les coefficients variants en fonction des modèles GR4H et GR4J sont donnés

\[{\eta _1} = \left\{ {\begin{array}{*{20}{l}}

{4/21}&{,{\rm{ si GR4H}}}\\

{4/9}&{,{\mkern 1mu} {\rm{ si GR4J}}}

\end{array}} \right.\]

\[{\eta _2} = \left\{ {\begin{array}{*{20}{l}}

{1.25}&{,{\rm{ si GR4H}}}\\

{2.5}&{,{\mkern 1mu} {\rm{ si GR4J}}}

\end{array}} \right.\]

• 1 module de production pour modéliser l’état du sol

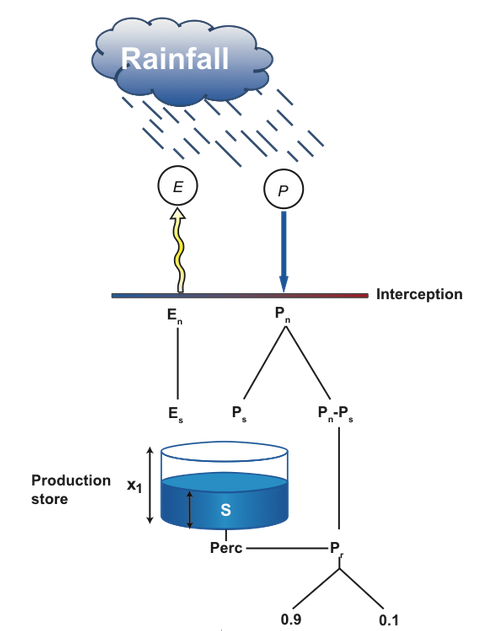
Figure 16 Schéma des procédures dans le module sol

Tout d’abord, en partant des pluies données en entrée du modèle $x$ et l’évapotranspiration potentielle ${e_p}$, au pas de temps $n$ les pluies et évapotranspirations nettes sont définies comme étant respectivement

\[P_{{\rm{net}}}^n = \max (0;\;{x^n} - e_p^n{\rm{\;}})\]

\[E_{{\rm{net}}}^n = \max (0;\;e_p^n - x{{\rm{\;}}^n})\]

Ces équations signifient qu’une partie des pluies sont interceptées et converties en évapotranspiration. Une partie de ces pluies sera directement transmise tandis que la partie restante ${P_s}$ soumise au taux d’évaporation réelle ${E_s}$ ira dans un réservoir de production et ne sera rendue en sortie qu’après percolation ${P_{{\rm{erc}}}}$. L’évaporation sera donc perdue.

Dès lors, en considérant que ces variables varient de façon parabolique, elles auront une solution de la forme suivante

\[P_s^n = \frac{{{X_1}\left[ {1 - {{\left( {\frac{{{S^{n - 1}}}}{{{X_1}}}} \right)}^2}} \right]\;\tanh \left( {\frac{{P_{{\rm{net}}}^n}}{{{X_1}}}} \right)}}{{1 + \frac{{{S^{n - 1}}}}{{{X_1}}}\;\tanh \left( {\frac{{P_{{\rm{net}}}^n}}{{{X_1}}}} \right)}}\]

\[E_s^n = \frac{{{S^{n - 1}}\left[ {2 - {{\left( {\frac{{{S^{n - 1}}}}{{{X_1}}}} \right)}^2}} \right]\;\tanh \left( {\frac{{E_{{\rm{net}}}^n}}{{{X_1}}}} \right)}}{{1 + \left( {1 - \frac{{{S^{n - 1}}}}{{{X_1}}}} \right)\;\tanh \left( {\frac{{E_{{\rm{net}}}^n}}{{{X_1}}}} \right)}}\]

Une partie des pluies alimentera le réservoir de production dont la capacité est représentée par le paramètre ${X_1}$. Il est important de noter que, par approximation numérique, les deux variables dépendent de façon explicite du volume dans le réservoir c’est-à-dire avant ajout de ces valeurs.

Le volume dans le réservoir au pas de temps intermédiaire $n - 1/2$, juste avant la percolation, est noté ${S^{n - 1/2}}$ et sera évalué par la formule

\[{S^{n - 1/2}} = {S^{n - 1}} - E_s^n + P_s^n\]

Le débit sortant de ce réservoir est donné par la percolation qui suivra une loi de puissance qui est fonction du volume dans le réservoir après application des pluies et de l’évapotranspiration. Dans la formule suivante, un coefficient ${\eta _1}$ ajuste cette loi pour l’adapter au pas de temps choisi. C’est la première différence entre le modèle GR4H et le modèle GR4J.

\[P_{{\rm{erc}}}^n = {S^{n - 1/2}}\;\left\{ {1 - \left[ {1 + \left( {{\eta _1}\;\frac{{{S^n}}}{{{X_1}}}} \right)} \right]} \right\}\].

La volume final dans le réservoir sera actualisé avec

\[{S^n} = {S^{n - 1/2}} - P_{{\rm{erc}}}^n\].

Le débit total de ce module regroupe les débits fournis par le réservoir de production et la fraction de pluie directement transmise.

\[P_r^n = P_{{\rm{erc}}}^n + (P_{{\rm{net}}}^n - P_s^n)\]

Les débits en sortie de ce module seront décomposés selon deux composantes ${P_9}$ et ${P_1}$ :

\[\left\{ {\begin{array}{*{20}{l}}

{P_9^n}&{ = 0.9\;P_r^n}\\

{P_1^n}&{ = 0.1\;P_r^n}

\end{array}} \right.\]

Les pertes en sortie de ce modèle sont données par la véritable évapotranspiration, telle que

\[e_a^n = E_s^n\]

• 2 modules de transfert composés d’hydrogrammes unitaires

Figure 17 Aspect de l’UH1

Figure 18 Aspect de l’UH2

Les deux débits produits seront transmis par le biais de deux hydrogrammes unitaires différents dont les durées sont déterminées par le paramètre ${X_4}$ ; Cependant, l’hydrogramme UH1 possède un temps de base de ${X_4}$, tandis que UH2 est formé avec un temps de base deux fois plus grand. Ces hydrogrammes unitaires sont sensé simuler le temps de déphasage entre les évènements de pluie et les débits transmis à l’exutoire. Leurs aspects vont également dépendre du pas de temps choisi C’est la deuxième et dernière différence entre les modèles GR4H et GR4J. Les formules de ces deux hydrogrammes unitaires sont données ci-dessous et écrites sous une forme plus compacte mais équivalente à celles formulée par C. Perrin et al.[4] et T. Mathevet [5] :

\[{\rm{UH1}} = {\xi _1}\;{\eta _2}\;{\left( {\frac{t}{{X4}}} \right)^{{\eta _2} - 1}}\],

\[{\rm{UH2}} = {\xi _2}\;\frac{{{\eta _2}}}{2}\;{\left( {\frac{t}{{X4}}} \right)^{{\eta _2} - 1}}\],

avec ${\xi _1}$ et ${\xi _2}$ les fonctions  discrètes suivantes

En appliquant la définition suivante de la norme

on obtient les formes normalisée suivantes

Dès lors, les débits à la sortie de chaque module seront respectivement les convolutions entre les hydrogrammes unitaires et les entrées de chaque module

\[Q_9^n = {\rm{UH1}}\;*\;P_9^n\],

\[Q_1^n = {\rm{UH2}}*\;{P_1}^n\].

• 1 module de production de routage

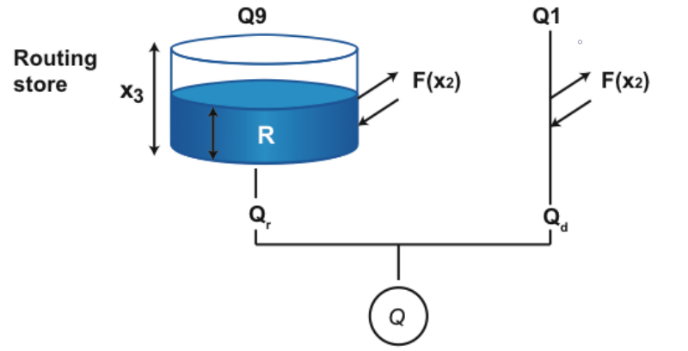
Figure 19 Schéma des procédures dans le module production de routage

Dans ce module, les deux entrées seront fournies à la suite des deux hydrogrammes unitaires des modules de transfert. Ces deux débits emprunteront des chemins différents. Le débit Q9, la plus grande partie des débits, est soumis à un réservoir de routage tandis que le deuxième sera directement transmis en sortie. La raison pour laquelle ces deux branches appartiennent au même module se trouve dans la présence de perte de débits, provoqués par des échanges entre bassins, sur ces ceux chemins. Ces échanges dépendront du paramètre ${X_2}$, mais également du taux de remplissage du bassin de routage. Il est important de noter que même le débit ${Q_1}$, ne passant pourtant pas par ce bassin, dépendra indirectement de l’état de celui-ci.

Les échanges $F$ seront donné par la formule ci-dessous et dépendra du niveau de remplissage du bassin de routage avant ajout des débits :

\[{F^n} = {X_2}{\left( {\frac{{{R^{n - 1}}}}{{{X_3}}}} \right)^{7/2}}\].

Le niveau d’eau actualisé pour estimer les débits à la sortie du réservoir est estimé :

\[{R^{n - 1/2}} = \max (0;\;{R^{n - 1}} + Q_9^n + {F^n})\].

Le débit à la sortie du réservoir suivra une loi identique à celle formulée dans l’Equation

\[Q_r^n = {R^{n - 1/2}}\left\{ {1 - {{\left[ {1 + {{\left( {\frac{{{R^{n - 1/2}}}}{{{X_3}}}} \right)}^4}} \right]}^{ - 1/4}}} \right\}\].

Le niveau final dans le réservoir sera

\[{R^n} = {R^{n - 1/2}} - Q_r^n\].

Dans la deuxième branche, le débit ${Q_1}$ sera directement transmis en ajoutant les échanges

\[{Q_d} = \max (0;\;Q_1^n + {F^n})\].

Les pertes ou apports dans ce module seront donnés par la valeur et le signe de ${F^n}$.

• 1 module de bilanLa relation regroupant tous les flux est directe. Tous les débits sont additionnés pour obtenir le débit à l’exutoire.

\[{Q^n} = Q_r^n + Q_d^n\]

\[{\rm{Outlet}} = {Q^n}\]

Modèles maillés - gridded

Dans ces modèles, les bassins versants étudiés seront découpés en plusieurs cellules ou mailles qui vont communiquer entre elles. Chacune de ces cellules possède leurs propres caractéristiques.

Modèle Adali

Une première approche d’un modèle distribué est appréhendée avec la méthode Adali. Dans ce modèle très simple, les débits sont estimés en deux grandes étapes de calcul déjà mentionnées à plusieurs reprises dans les précédents chapitres :

• L’estimation des coefficients de ruissellement en chaque maille (cf. Section 2.2.3)

• L’estimation des vitesses de propagation sur chaque maille (cf Section 2.2.4).

Les hypothèses à prendre en compte pour appliquer ce type de modèle sont identiques à celles déjà énoncées dans ces deux sections. A celles-ci peuvent être ajoutés :

• Les coefficients de ruissellement sont donnés dans le Tableau 1. Ces valeurs ne sont pas continues et dépendent de paramètres qui ont été calibrés dans le cadre du projet Adali ;

• Les vitesses stationnaires moyennes d’écoulement dépendent uniquement des pentes et du type de sol.

Les valeurs sont estimées dans le Tableau 2

Coefficient de ru issellement (Adali) [-]
O ccupation	Pentes
	≤ 4%	≤ 8%	≤ 16%	> 16.0%
Forêts	0.03	0.04	0.05	0.06
Prairies*	0.045	0.055	0.065	0.0753
Cultures*	0.063	0.073	0.093	0.103
Urbains	0.17	0.18	0.19	0.2
Rivières*	0.2	0.2	0.2	0.2
Eau	1	1	1	1

Tableau 1 Coefficients de ruissellement Adali

Vitesse de ru issellement (Adali) [m/s]
O ccupation	Pentes
	≤ 4%	≤ 8%	≤ 16%	> 16.0%
Forêts	0.15	0.2	0.25	0.3
Prairies*	0.3	0.4	0.5	0.6
Cultures*	0.35	0.45	0.55	0.65
Urbains	0.45	0.55	0.65	0.75
Rivières*	0.55	0.65	0.75	0.85
Eau	0.35	0.45	0.55	0.65

Tableau 2 Vitesses de ruissellement Adali en [m/s]

Cette méthode est surtout employée dans l’étude de petits bassins versants en région Wallonne (développée pour la Province du Brabant Wallon) et ainsi prévoir des débits pour des pluies statistiques à périodes de retour différentes.

L’avantage d’une telle méthode réside dans sa facilité d’application.

Cependant ces coefficients ne sont que des valeurs moyennes. Leurs valeurs peuvent très fortement varier d’un bassin à l’autre ou lors d’évènements météorologiques très différents comme des sécheresses ou des crues. En effet, lors de périodes de crues, les sols seront saturés en eaux, le coefficient d’infiltration sera donc faible. Lors de sécheresses, le phénomène est plus complexe. Le sol étant pauvre en eau, l’eau peut facilement, a priori, s’infiltrer plus facilement dans le sol. Mais, lors d’épisodes plus longs de sécheresse, ce même sol peut temporairement perdre sa capacité d’infiltration et ainsi provoquer du ruissellement. C’est l’ensemble de ces phénomènes qui ne seront pas représentés dans un tel modèle.

De plus, calibrer automatiquement de nouveaux coefficients avec cette méthode n’est pas aisé, compte-tenu du nombre de paramètres à déterminer. Ces paramètres n’évoluent pas de façon continue avec la pente. Rien ne peut donc garantir une convergence dans les méthodes d’optimisation.

Malgré toutes ces limitations, le modèle reste utile s’il est utilisé dans de bonnes conditions. Par exemple, il permet de simuler des évènements extrêmes et isolés, tels que des crues, en adaptant avec un facteur de proportionnalité les coefficients de ruissellement.

Modèle basé sur les nombres de Froude

Le modèle original, présenté dans cette section, propose une autre façon de calculer les vitesses de ruissellement. Ce modèle distribué recourt à un nombre adimensionnel adapté aux écoulements de surface pour évaluer la vitesse de l’eau transférée sur cette maille vers son voisin de plus grande pente. La pluie ou la portion de pluie reçue par un ou plusieurs voisins peut être déterminée par des coefficients de ruissellement comme dans la méthode Adali ou toute autre fonction de production.

Pour rappel, le nombre de Froude, noté $Fr$,est un nombre adimensionnel significatif pour l’étude d’écoulements à surface libre et sa valeur détermine notamment le régime de l’écoulement. Dans une section rectangulaire, le nombre de Froude est défini comme suit

\[Fr = \frac{u}{{\sqrt {gh} }}\]

où $u$ est la vitesse du flux, $g$ le champ gravitationnel local de la Terre. Le nombre de Froude peut être vu comme la comparaison entre l’inertie de flux et le champ gravitationnel ou encore la comparaison entre la vitesse moyenne de l’écoulement et la vitesse d’une onde de gravité.

Dans les simulations hydrologiques, la vitesse et la hauteur d’eau sont souvent des inconnues dans un problème. La pente locale est, quant à elle, la seule donnée qui peut être collectée a priori. C’est la raison pour laquelle les équations qui seront présentées ci-dessous, seront basées principalement sur les pentes pour distribuer une valeur de Froude en chaque maille $i$. Ces mailles sont définies avec une longueur $\Delta x$ le long de la direction vers laquelle le flux est transféré. Une distinction sera également faite entre les mailles rivières et les mailles bassins comme définies dans la Section 0. Par souci de simplicité, le symbole $\eta $ signifiera qu’un élément pourra être soit « rivière » soit « bassin ».

Dans ce modèle, 5 paramètres seront considérés pour caractériser le ruissellement :

• $Fr_{{\rm{min}}}^{{\rm{riv}}}$ le nombre de Froude minimum dans tous les éléments « rivières »,

• $Fr_{{\rm{max}}}^{{\rm{riv}}}$, le nombre de Froude maximum dans tous les éléments « rivières »,

• \[Fr_{{\rm{min}}}^{{\rm{basin}}}\], le nombre de Froude minimum dans tous les éléments « bassin »,

• $Fr_{{\rm{max}}}^{{\rm{bassin}}}$, le nombre de Froude maximum dans tous les éléments « bassin ».

• ${q_{{\rm{ref}}}}$ le débit de référence.

En partant de la définition du nombre de Froude, le débit ${q_i}$ évalué à une maille $i$ est donné par

\[{q_i} = F{r_i}\;\sqrt {g\;{h_i}} \;{h_i}\;{l_c}\],

avec ${l_c}$ la largeur caractéristique de l’écoulement. En isolant la hauteur d’eau ${h_i}$, on obtient l’expression

\[{h_i} = {\left( {\frac{{{q_i}}}{{F{r_i}\;\sqrt g }}} \right)^{2/3}}{\left( {\frac{1}{{{l_c}}}} \right)^{2/3}}\].

Pour trouver une solution à cette expression, il reste trois inconnues à déterminer. Pour la première, il s’agit de ${q_i}$ auquel est attribué une valeur liée à un débit de référence ${q_{{\rm{ref}}}}$, c’est-à-dire un des paramètres du modèle.

La deuxième inconnue est le nombre de Froude évalué localement. Pour l’estimer, l’hypothèse que ce nombre dépend uniquement de la pente locale ${s_i}$ est considérée et que sa valeur évolue linéairement entre deux bornes définies par les paramètres $Fr_{{\rm{min}}}^\eta $ et $Fr_{{\rm{max}}}^\eta $.

\[F{r_i} = Fr_{{\rm{min}}}^\eta + {\omega _i}\;\left( {Fr_{{\rm{max}}}^\eta - Fr_{{\rm{min}}}^\eta } \right)\].

Dans un écoulement à hauteur d’eau uniforme, la vitesse est fonction de la racine carrée de la pente locale ${u_i} \propto \sqrt {{s_i}} $. Dès lors, le coefficient ${\omega _i}$ est défini comme le rapport

\[{\omega _i} = \frac{{\sqrt {{s_i}} - \sqrt {s_{{\rm{min}}}^\eta } }}{{\sqrt {s_{{\rm{max}}}^\eta } - \sqrt {s_{{\rm{min}}}^\eta } }}\].

Finalement, la dernière inconnue est la largeur de la coupe transversale ${l_c}$ et la manière dont celle-ci sera calculée dépendra du type de cellule à évaluer. Dans une maille rivière, il a été observé que la largeur d’un cours d’eau était liée à la taille du bassin versant avec un facteur 0.8. Dans une maille bassin, la largeur va quant à elle varier en fonction du rapport surface drainée par la maille courante ${A_i}$ (autrement dit sa convergence) et sa dimension le long de l’écoulement comparée avec la surface totale du bassin versant ${A_{{\rm{tot}}}}$.

\[{l_c} = \left\{ {\begin{array}{*{20}{l}}

{\frac{{{A_{{\rm{tot}}}}}}{{\sqrt {{A_i}} /0.8}}}&{,{\rm{rivi\`e re}}}\\

{\frac{{{A_{{\rm{tot}}}}}}{{{A_i}/\Delta x}}}&{,{\mkern 1mu} {\rm{bassin}}}

\end{array}} \right.\]

Dès lors, la formule de la hauteur d’eau devient

\[{h_i} = {\left( {\frac{{{q_{{\rm{ref}}}}}}{{F{r_i}\;\sqrt g }}} \right)^{2/3}}{\left( {\frac{1}{{{l_c}}}} \right)^{2/3}}\].

Quel que soit le type de cellule considéré, la vitesse sera donnée par

\[{u_i} = F{r_i}\;\sqrt {g{\mkern 1mu} {h_i}} \].

Finalement, le temps ${t_i}$ nécessaire pour transférer un flux d’une cellule à une autre est calculé avec

\[{t_i} = \Delta x/{u_i}\].

\[\alpha \] est un paramètre prenant en compte la direction de la cellule de plus grande pente.

Une telle méthode a donné des résultats encourageants notamment lors de premières estimations des crues de juillet 2021 sur le bassin de la Vesdre.

Types de Simulation

« Lumped »

Dans ces simulations le bassin versant est étudié dans sa globalité. Les données en entrées (pluies, évapotranspiration, températures, etc.) doivent être valables pour tout le bassin. Si celles-ci sont à l’origine distribuées, une procédure leur sera appliquée pour les agglomérer. Les débits fournis en sortie seront uniquement évalués à l’exutoire.

Dès lors, pour de telles simulations, tous les modèles 0D peuvent directement être appliqués. C’est d’ailleurs leur fonction première. Chacun de leurs paramètres sera fixe pour l’ensemble du bassin.

La force de telles simulations réside dans leur rapidité et leur plus grande facilité à trouver les paramètres optimaux. Il est d’ailleurs souvent évoqué que leur capacité à produire des résultats de qualité est supérieure aux modèles plus complexes et distribués.

« Gridded »

Dans une simulation distribuée, il est attendu en entrées des données qui soient également spatialisées. Les modèles à favoriser sont donc des modèles maillés. Il est néanmoins possible d’appliquer des modèles 0D à chacune des mailles si une loi de propagation ou d’échange entre les mailles est ajoutée. Ce type de procédures est, par exemple, déjà utilisé dans le modèle GRD qui est une application spatialisée du modèle GR5H.

De telles simulations sont souvent coûteuses en temps et complexes à calibrer. Cependant, elles permettent une meilleure prise en compte de la configuration et des particularités de chaque bassin. Ces types de modèle sont d’ailleurs les plus adaptés pour appliquer des modèles physiquement basés. La valeur des paramètres aura donc une véritable signification pour qu’ils puissent être plus faciles à interpréter ou contester.

Semi-distribuée

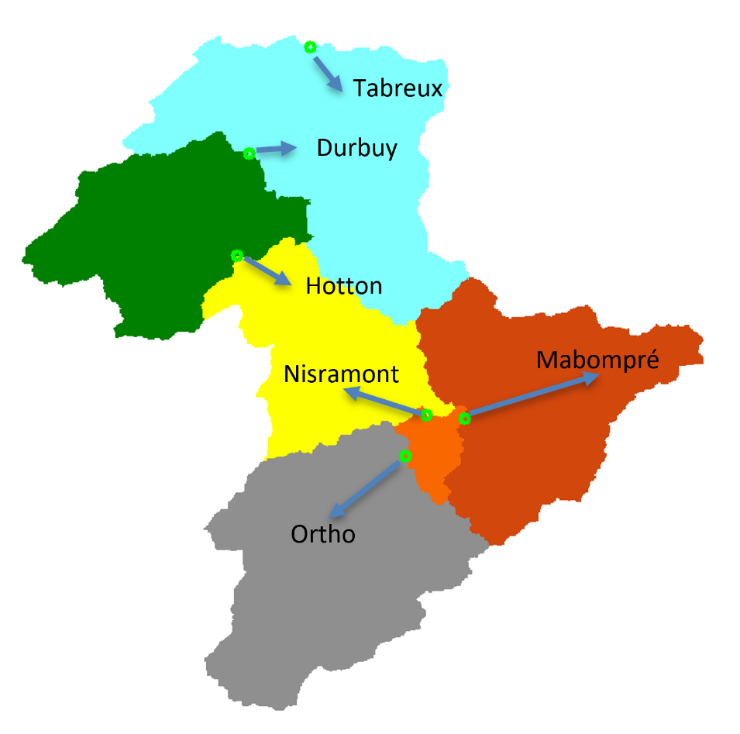
Pour allier l’efficacité et la rapidité des modèles « lumped » avec la précision et la prise en compte des particularités propres à chaque bassin versant, les simulations semi-distribuées apparaissent comme une bonne alternative. Si plusieurs stations de mesures de débits ou de hauteurs d’eau sont présentes dans un sous-bassin, il également intéressant de les utiliser comme comparaison dans la calibration des paramètres ou pour une évaluation simple de la qualité de la simulation. De plus, un bassin versant peut abriter une série de constructions humaines ou particularités pouvant modifier le comportement hydrologique naturel du bassin et perturber le bon fonctionnement de toute simulation « lumped ». Ce type de simulation est également utile lors d’études de dimensionnement de bassins d’orage ou de barrages.

Dans une simulation semi-distribuée, le bassin versant est divisé en sous-bassins n’admettant pas de chevauchement. Cette division est réalisée par le biais de points intérieurs définis par l’utilisateur et qui deviennent les nouveaux exutoires. A chaque sous-bassin, il est possible d’appliquer :

• un modèle 0D : chaque sous-bassin est traité de façon indépendante et possède son propre jeu de paramètres. L’évolution des propriétés physiques entre les régions du bassin peut ainsi éventuellement être mieux représentée ;

• un modèle maillé : les mailles appartenant à chaque sous-bassin sont isolées et une évaluation intermédiaire des débits est réalisée à chaque exutoire.

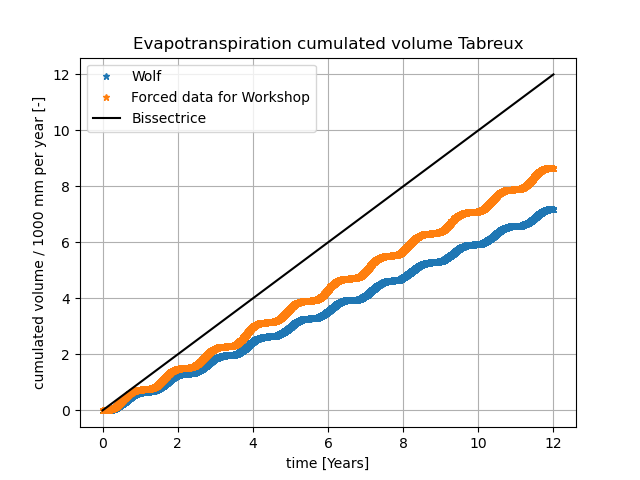
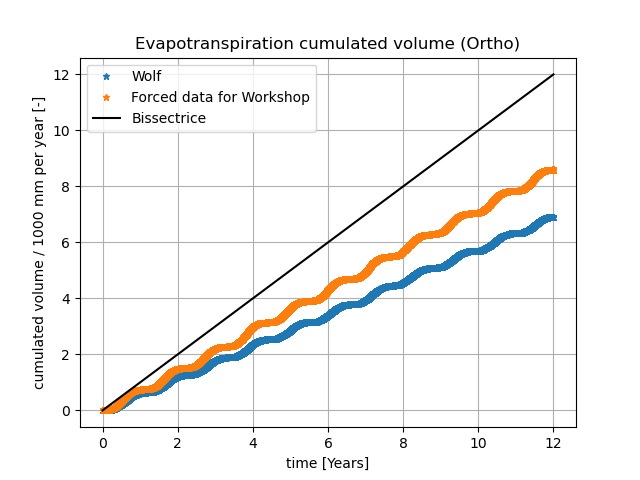
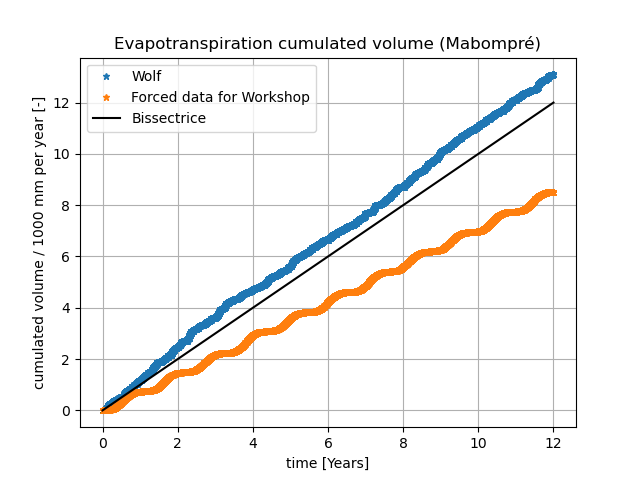
Figure 20 Bassin de l’Ourthe jusque Tabreux en semi-distribué

Le code de post-traitement Python est capable d’exploiter automatiquement tous ces sous-bassins pour reconstruire un hydrogramme à l’exutoire de l’entièreté du bassin versant.

Pour ce faire, l’utilisateur doit fournir un fichier « Catchment.posPro » permettant de reconstruire le réseau de rivières et ainsi générer automatiquement un arbre topologique représentant la manière dont les sous-bassins sont combinés pour reconstruire le bassin versant.

A ce stade il manque cependant encore une information : la loi de propagation entre les flux des différents sous-bassins. Le temps de propagation peut soit être directement donné par la matrice de temps écrite par le code Fortran soit par une loi d’écoulement plus complexe fournie par l’utilisateur. Par exemple, dans le modèle GRSD, une formulation semi-distribuée de GR5J/H, la loi de propagation est directement fonction d’un paramètre de célérité à déterminer ou calibrer par l’utilisateur et des débits amont. Il est également possible d’utiliser ces hydrogrammes partiels comme donnée d’entrée si celui-ci désire lancer une simulation numérique 1D ou 2D avec WOLF ou ses propres logiciels.

L’utilisateur a également la possibilité d’ajouter des bassins d’orage à ce réseau. Ceux-ci sont décomposés en deux flux :

• Un flux direct : se déversant complètement dans le bassin d’orage et remplissant celui-ci.

• Un flux indirect : sur lequel une partie du débit sera écrêté et transmis à l’aval. Tandis que le surplus est transféré dans le bassin d’orage.

Dès lors, il est nécessaire d’avoir une loi d’écrêtage et une loi de hauteur-débit à appliquer au bassin d’orage pour déterminer le débit sortant de celui-ci et l’ajouter au débit aval. Certaines de ces lois sont déjà disponibles dans le code Python pour différentes configurations bien connues (ajutage circulaire, rectangulaire, déversoir seuil épais, seuil mince, triangulaire…). Il est cependant très facile pour l’utilisateur d’adapter et de compléter ces lois en ajoutant par exemple le véritable système de contrôle de régulation du barrage étudié.

Post-traitement d’un modèle semi-distribué

Glossaire

• Exutoire partiel = Point intérieur = Junction « J »

• Elément anthropique = Retention Basin « RB »

• Sous-bassin = bassin versant lié à un point intérieur

Fonctionnement général

Le code de post-traitement, écrit en Python3, possède de multiples rôles. Dans une approche semi-distribuée, il va hiérarchiser les différents sous-bassins selon la topologie définie par le modélisateur. Cette topologie peut être une vue en arbre simple (succession de confluences) ou une approche maillée (confluences et diffluences). Sur cette base, il va lire les résultats fournis par le code Fortran, éventuellement leur appliquer de nouveaux traitements et les combiner pour obtenir des hydrogrammes à chaque exutoire. Il a logiquement la charge de tracer des graphiques selon différents formats permettant la visualisation et l’interprétation visuelle. Ce code est également capable de comparer différentes simulations entre elles : soit en appliquant des reconstructions différentes des résultats d’une même simulation, soit en récupérant les résultats issus d’une autre simulation du code Fortran.

Les valeurs numériques sont traitées selon le Système International ([m³/s] pour les débits, [mm/h] pour les pluies, [km²] pour les surfaces de BV…). Les fuseaux horaires sont également uniformisés en GMT/UTC+0.

Deux types de modules ou objet existent :

• Le module « sous-bassin » : regroupant les éléments hydrologiques calculés par le Fortran

• Le module « élément anthropique » : un bassin d’orage, un barrage-réservoir ou toute structure nécessitant un traitement numérique particulier (stockage local, séparation de flux…)

Ceux-ci seront expliqués plus en détail dans les sections à venir.

Organisation sur disque d’une simulation

Une modélisation hydrologique est contenue dans un répertoire du disque dur. Ce dernier est organisé en sous-répertoires :

• « Characteristic_maps » : lieu de stockage des données de base et des informations dérivées du bassin versant général

• « Whole_basin » : lieu de stockage des pluies et évapotranspiration utiles pour la simulation, y compris la discrétisation spatiale (format WOLF et shapefile)

• « Subbasin_X » : lieu de stockage des traitements et résultats partiels du sous-bassin n°X (ATTENTION : le numéro du sous-bassin peut être différent de celui du point intérieur)

• « PostProcess » : lieu de stockage des résultats du post-traitement PythonLes données générales (topographie, occupation du sol…) à l’échelle de la région peuvent/doivent être accessibles depuis la machine de calcul mais ne doivent pas être copiées dans le répertoire de simulation.

Leur accès est identifié via le fichier de paramètres.

Pour la plupart, le code Fortran réalisera une opération de « crop/merge » pour les obtenir sur l’emprise spatiale stricte du modèle.

Chaque simulation contiendra par défaut un fichier « Input.posPro »

Le nom d’un fichier sorti par le code post-traitement Python aura la structure suivante : « nom de la simulation » + « _ »+ « type_de_simulation » + « _ » + « nom de l’intersection ».Fichiers d’entrée

Organisation sur disque de scénarios

Scénario « hydrologique »

Chaque modification dans le fichier de paramètres de la modélisation hydrologique revient à définir un nouveau scénario. Dès lors, tout nouveau scénario doit être stocké dans un répertoire distinct.

Il peut être logique d’organiser ces scénarios dans un même répertoire mais ce choix est laissé à l’utilisateur. La distribution des scénarios peut donc s’envisager sur une même machine sur des disques séparés ou sur des machines distinctes, pour autant qu’elles soient accessibles via le réseau. La vitesse d’importation des fichiers est bien entendu dépendante de la structure retenue et de la vitesse de l’infrastructure réseau le cas échéant.

Scénario « anthropique » ou « topologique »

Un scénario anthropique est lié au paramétrage des ouvrages qui dépendent du calcul de post-process ou alors de liaison topologique des sous-bassins.

Ce type de scénario n’a pas besoin de multiplier les répertoires de simulation. Il suffit dans ce cas de multiplier les fichiers de paramètres. Comme décrit précédemment, les fichiers de résultats seront identifiés sur base du nom de scénario indiqué.

Comparaison de scénarios

L’outil de comparaison demande à l’utilisateur de fournir tous les chemins d’accès aux résultats à comparer, en absolu ou en relatif. Là encore, il peut paraître logique d’utiliser une structure simple de répertoires imbriqués mais il est toujours possible d’exploiter un réseau informatique pour combiner différentes sources de calcul et de stockage.

Topologie

La topologie du modèle se base sur deux fichiers :

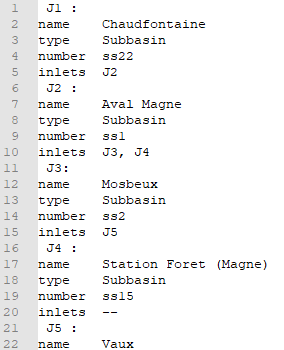
• Un fichier dont le nom par défaut est « Catchment.postPro » regroupant toutes les sous-bassins et autres éléments de gestion des flux. Le nom de fichier peut cependant être personnalisé afin de tester différents scénarios topologiques pour une même simulation hydrologique issue du code Fortran.Chaque élément constitue un groupe de paramètres identifié par une valeur entière unique précédée de « J ».

Les paramètres obligatoires sont :

• « name » : un nom/label explicite de l’élément

• « type » : « Subbasin » (bassin naturel) ou « RB » (structure anthropique)

• « number » : l’index du sous-bassin sur base de la numérotation des points intérieurs (pour un objet de type « Subbasin »). Cet index est précédé de « ss ».

• « inlets » : une liste séparée par des virgules énumérant les éléments en amont. S’il s’agit d’une tête de bassin, il faut indiquer « – » (double tiret). Pour un ouvrage, ces flux seront utilisés comme sollicitation de l’ouvrage d’entrée (à ne pas confondre avec des flux directs dans la retenue).

Exemples :

Des paramètres supplémentaires peuvent être ajoutés pour un objet de type « RB :

• « type of RB » : le type d’ouvrage« direct inside RB » : les flux à

  traiter comme arrivant directement dans la retenueUn fichier dont le nom par défaut est « RetentionBasins.postPro » ou tout autre fichier d’extension « .postPro » regroupant toutes les structures anthropiques. Chaque ouvrage constitue un groupe de paramètres identifié par une valeur entière unique accompagné du préfixe « RB ». Ici seront stockés tous les paramètres nécessaires à chacune des structures. Leurs nombres et noms dépendront du type de celle-ci mais la liaison à la topologie générale se fera vie le champ « from. » dont la valeur doit renvoyer vers un élément « Jx » valide.

• « outlets » : une liste des éléments aval et leurs noms si

  plusieurs sont présents.

Détermination de l’arbre topologique

Dans cet algorithme, la structure du réseau hydrologique/hydraulique est construit en regroupant tous les éléments simulés avec le Fortran et en y ajoutant des modules anthropiques de manière à représenter le plus fidèlement possible toutes les particularités du bassin versant.

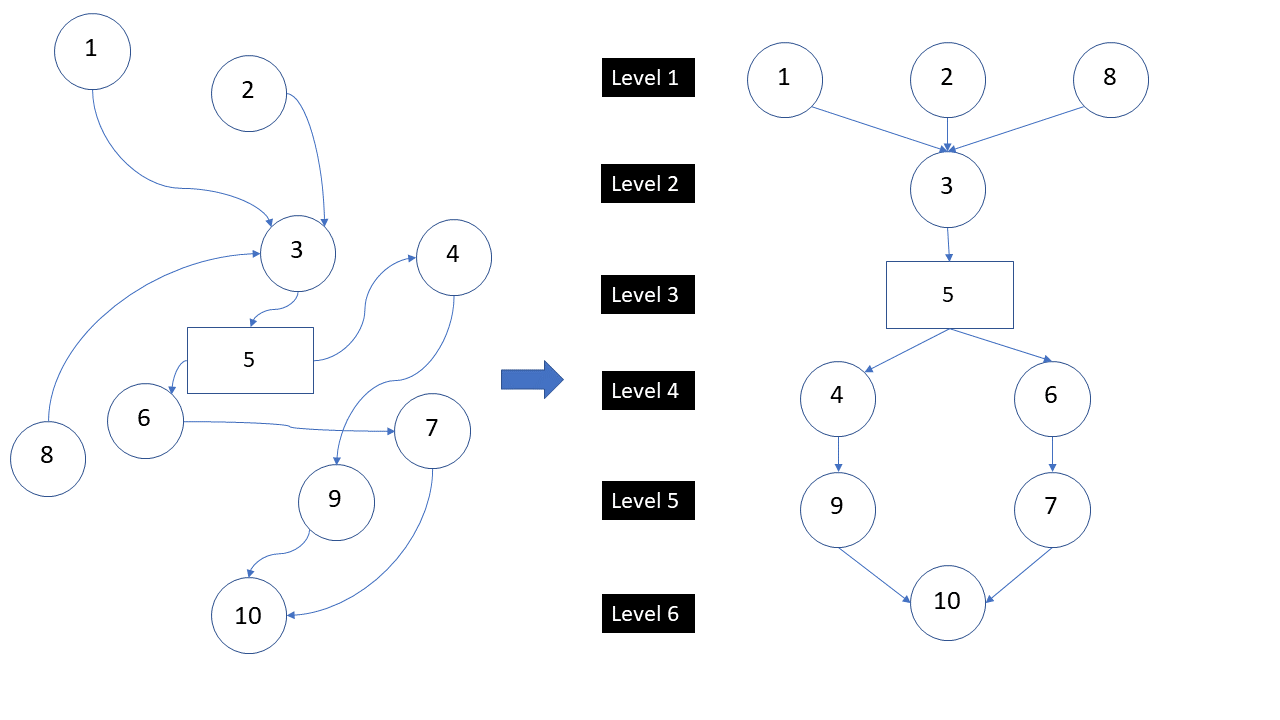
L’objectif est de pouvoir calculer les hydrogrammes en tout point en ne parcourant qu’une seule fois ce réseau. Pour ce faire, un graphe topologique acyclique avec différents niveaux est nécessaire. Le niveau le plus bas représente les éléments les plus en amont (têtes de bassin), tandis que le dernier niveau contiendra le sous-bassin dont l’exutoire est confondu avec celui du bassin versant global.

Figure 21 Exemple de hiérarchisation par niveau d’un bassin versant complexe en apparence. Les sous-bassins sont représentés par des cercles et les modules anthropiques par des rectangles.

Les avantages d’une telle structure hiérarchisée sont multiples. Tout d’abord, cette organisation octroie une plus grande clarté vis-à-vis de la dépendance des modules entre eux, comme représenté sur l’exemple à la Figure 21. De ce fait, elle garantit qu’un élément présent sur un niveau soit uniquement dépendant des niveaux inférieurs. Cela implique un gain de temps lors de la reconstruction des hydrogrammes, mais aussi une plus grande maniabilité de ceux-ci. En effet, si plusieurs éléments sont modifiés a posteriori, et que le niveau le plus bas de ceux-ci est localisé, par exemple, sur le troisième niveau, alors les hydrogrammes impactés seront uniquement ceux de niveaux supérieurs.

Sur le premier niveau, il n’est donc possible de trouver que des sous-bassins et aucun élément anthropique. Ces sous-bassins n’ont aucun élément à leur amont. Il s’agit des têtes de bassin.

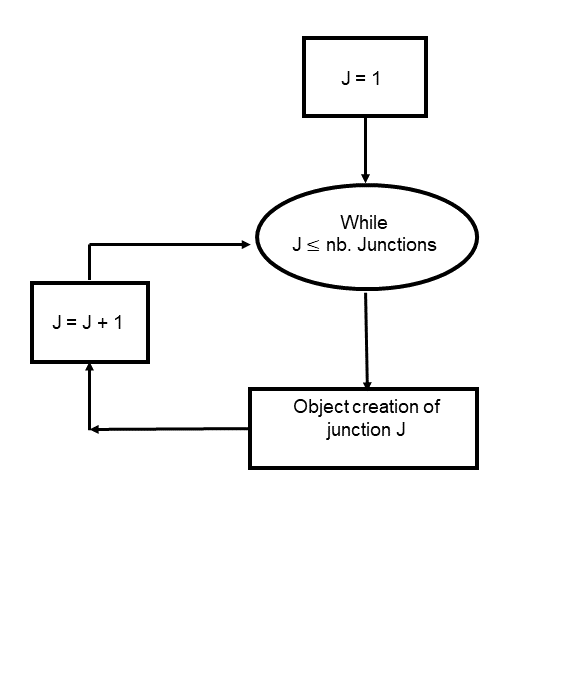
Le script commence par lire les fichiers « .postPro » de la topologie et les convertit en dictionnaire. L’arbre de topologie peut ensuite être construit sur base de 2 parcours de l’ensemble des éléments :

1. les objets sont créés et initialisés. Le niveau par défaut est 1.

2. les éléments sont liés entre eux et les têtes de bassin sont identifiées et placées dans le premier niveau du dictionnaire topologique. Le niveau des autres éléments est incrémenté d’une unité et ainsi temporairement rangés dans le deuxième niveau.

Figure 22 Flowchart de la première lecture du fichier topologique

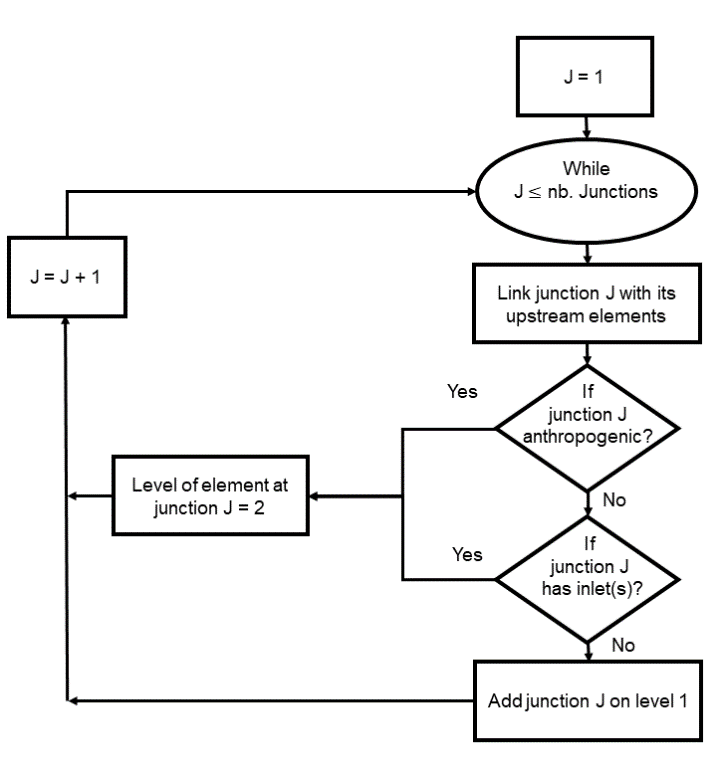
Figure 23 Flowchart de la deuxième lecture du fichier topologique

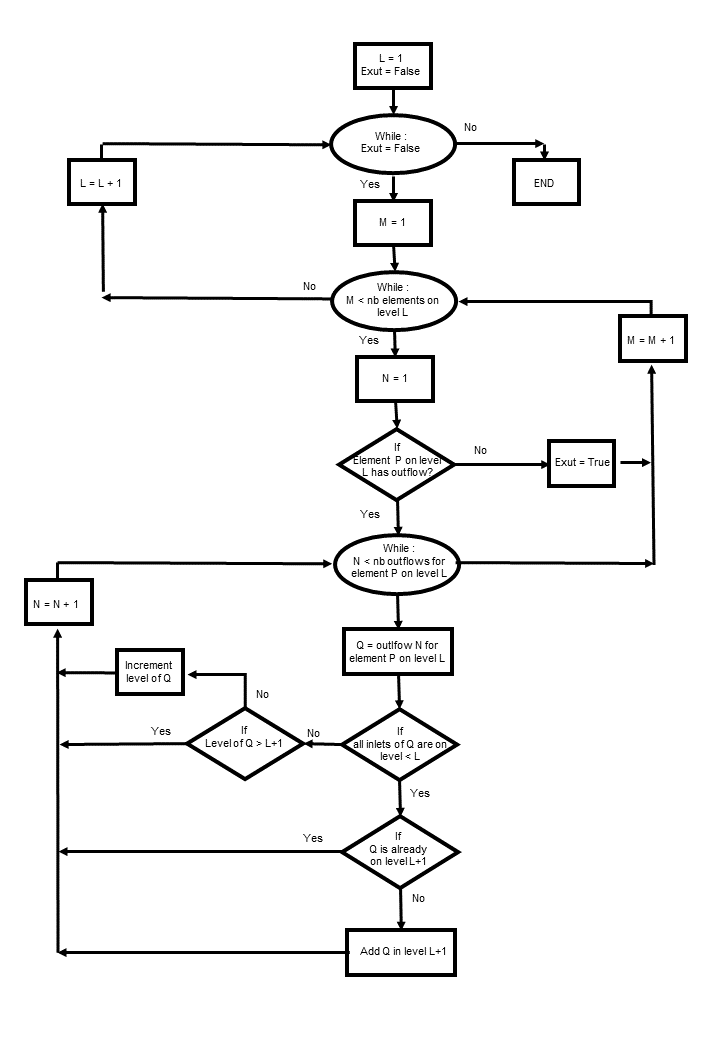
Finalement, pour construire le graphe topologique et en partant de la première couche :

1. Un nouveau niveau est créé jusqu’à ce que l’élément du niveau examiné ne possède plus d’élément aval. 2. A chaque niveau courant, tous les éléments aval des objets sont incrémentés et analysés. S’ils sont tous sur un niveau identique ou supérieur au niveau courant, celui-ci est ajouté au niveau suivant. Avant de réaliser l’opération précitée, un même élément pouvant être parcouru plusieurs fois, il est important de vérifier que cette opération n’ait pas déjà été réalisée au préalable sur ce même niveau.

Cet algorithme assure qu’un élément de niveau inférieur possédera toujours tous les éléments nécessaires pour construire ou calculer des éléments de niveau supérieur.

Une représentation graphique est automatiquement tracée afin que l’utilisateur vérifie son réseau.

Figure 24 Flowchart de l’algorithme de complétion du réseau tolopologique

Exécution du code post-traitement

Au démarrage du code, l’utilisateur devra choisir le fichier de travail qui sera associé à la variable « filename». Ce fichier peut uniquement posséder les deux types d’extension (celle-ci doit être spécifiée lors de la recherche) ci-dessous :

1. « Input.postPro » : Une seule configuration/simulation soit être traitée. Ce fichier reprend les fichiers de topologie à lire ainsi que les opérations à réaliser. Sur base de ceux-ci, le code affichera automatiquement une fichier PDF représentant graphiquement le réseau. Il sera demandé à l’utilisateur si celui-ci correspond à ses attentes. Dans l’affirmative, le code génère les hydrogrammes de tous les sous-bassins ainsi que les hydrogrammes à chaque intersection.

2. « Input.compar » : Si ce fichier est présent dans le dossier indiqué, celui-ci aura la priorité de lecture. Le code effectuera une comparaison de simulations ou configurations différentes et, ainsi, les comparer. Dans ce fichier seront regroupés tous les autres fichiers «.postPro » à lire, et utiles à la comparaison

Stockage mémoire des hydrogrammes partiels

Quel que soit le module, différents hydrogrammes sont gérés en mémoire par un dictionnaire Python composé de sous-dictionnaires de sortie dont les clefs doivent être uniques et peuvent être soit le numéro de la jonction, soit le numéro du point intérieur accompagné du préfixe « ss », soit le nom attribué à l’élément. Celui-ci est déterminé à la deuxième lecture du fichier topologique, lors de la connexion entre les différents éléments. Le nom attribué par défaut à cette clef est « DEFAULT ». Ces sous-dictionnaires contiennent eux-mêmes deux clefs:

• « Net » qui contient un vecteur avec les débits calculés ou forcés à cette sortie.

• « Raw » qui contient un vecteur avec les débits naturels. Ce flux serait égal au débit simulé si aucune intervention humaine n’était présente.

Pour tous les hydrogrammes, le temps de référence sera celui de l’exutoire général du bassin versant. Cette référence commune permet d’obtenir le résultat final par simple addition des vecteurs partiels ; la gestion des décalages temporels étant déjà prise en compte.

Module sous-bassin (SubBasin)

Comme mentionné précédemment, le module sous-bassin interprète et reconstruit les résultats simulés par le code Fortran. Dans ce module seront stockés les hydrogrammes, la pluie et potentiellement l’évapotranspiration et toute autre donnée de bassin. Parmi les propriétés intrinsèques à ce module, plusieurs sont remarquables comme :

• la surface [km²] drainée par le sous-bassin ;

• le fuseau horaire considéré (GMT/UTC) dans les hydrogrammes sortis par le code Fortran. Tout résultat fourni par le code Python sera en GMT+0, sauf demande différente de l’utilisateur ;

• le temps de transfert [s] (« time delay ») représentera le temps nécessaire pour que son hydrogramme soit transmis à l’exutoire du bassin versant total.

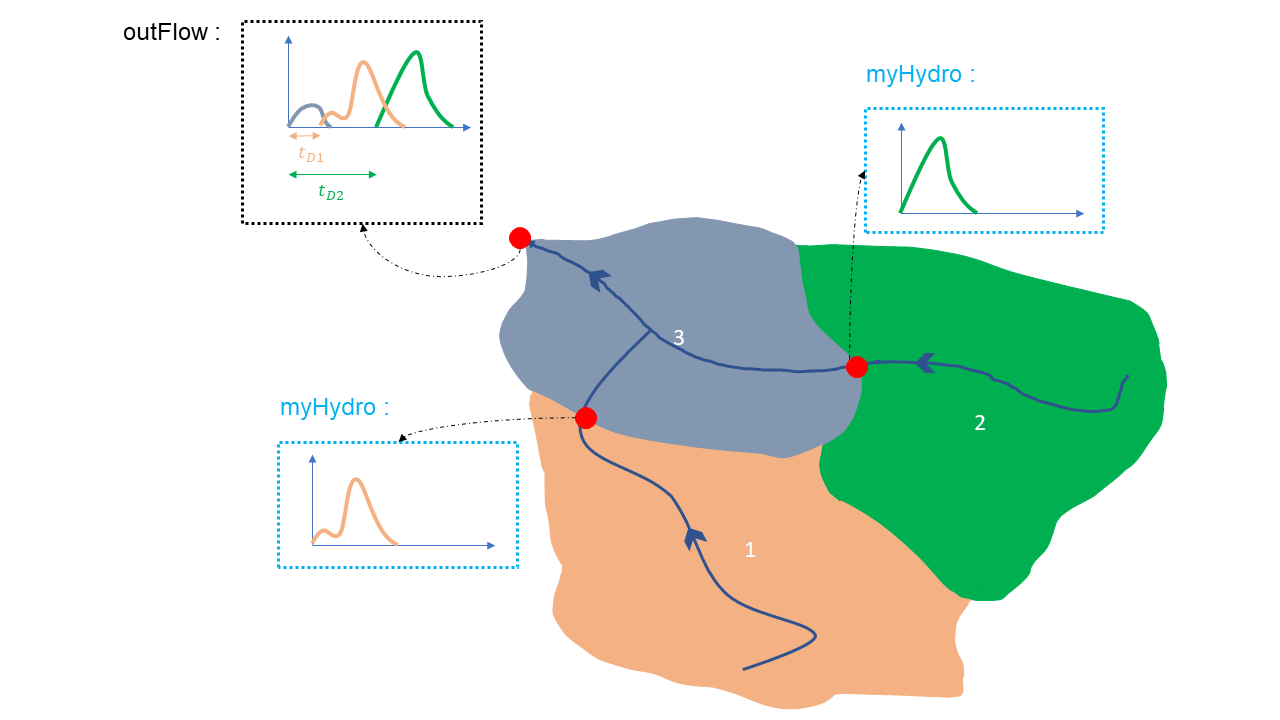
Figure 25 Représentation schématique d’un bassin versant et du décalage « time delay », noté \(t_{D}\), à apppliquer aux hydrogrammes « myHydro » des sous-bassins pour obtenir les hydrogrammes « outFlow ».

Un hydrogramme supplémentaire et propre à ce type de module, représenté par la variable « myHydro », est sauvegardé dans cet objet. Celle-ci sera une matrice contenant les hydrogrammes bruts du sous-bassin. Le nombre de colonnes sera égal au nombre couches présentes dans la simulation (par exemple, le modèle VHM en contiendra trois). Pour construire le vecteur « outFlow », il suffira d’additionner cette variable dans tous les éléments amont et d’y ajouter la variable « myHydro », propre au sous-bassin, en tenant compte du décalage temporel « time delay », comme représenté sur Figure 2525.

Il est important de noter qu’ici le dictionnaire « outFlow » ne contiendra qu’un seul élément, car un sous-bassin ne peut posséder qu’un seul exutoire. Ce module ne pourra jamais être responsable d’une différence entre les vecteurs « Net » et « Raw ».

Module anthropique

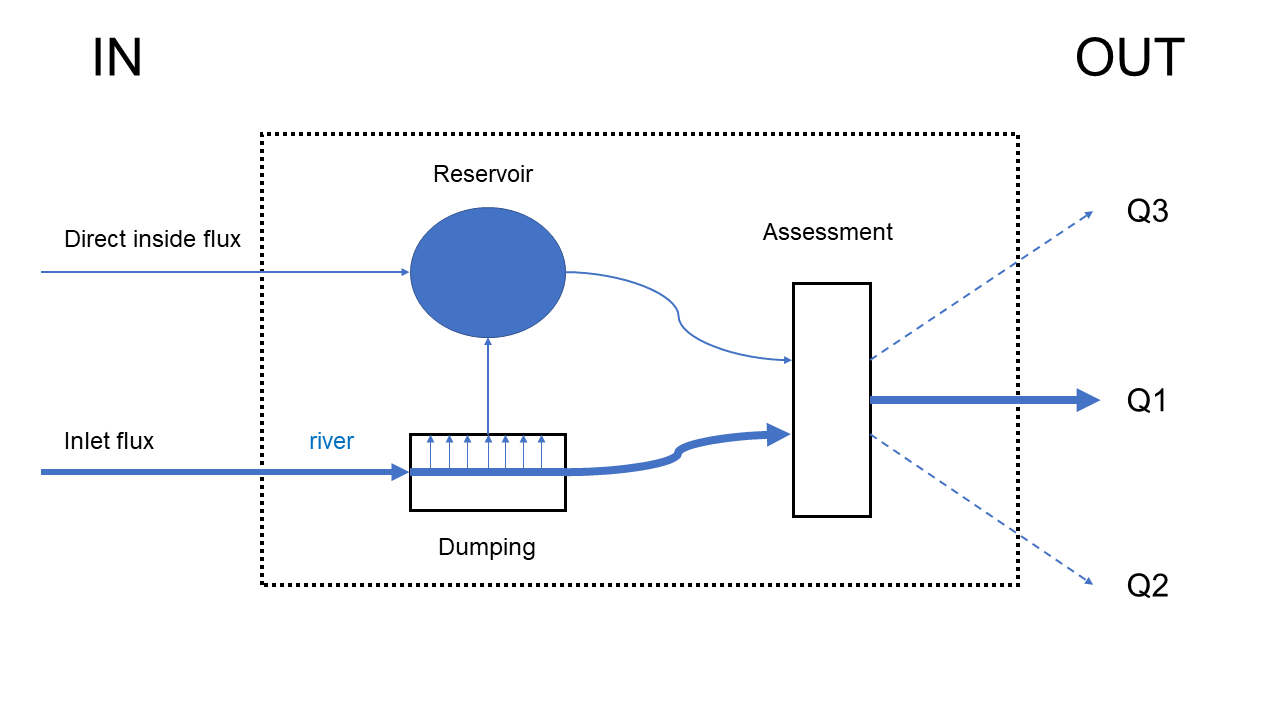
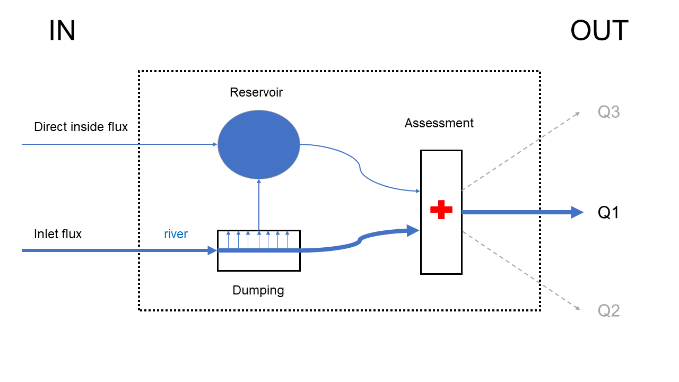
Figure 26 Forme générale des éléments composant le module anthropique

Ce module sera constitué de deux flux en entrée qui seront attribués à chacune des composantes internes du module. Celles-ci peuvent être vues schématiquement comme :

• Une rivière

• Un réservoir

Les deux peuvent communiquer entre elles :

• La rivière peut être écrêtée (« dumping ») selon une loi de débit ou de hauteur choisie par l’utilisateur.

• Le réservoir se remplira progressivement par bilan de masse grâce aux entrées directes dans celui-ci, et des débits écrêtés depuis la rivière. La sortie du réservoir est déterminée par une loi de hauteur-débit.

• Une fonction (« assessment ») qui combine les deux points précédents pour générer un débit de sortie principal (Q1) et potentiellement des débits additionnels (Q2, Q3, …).

Dans tous les cas cités précédemment, il est possible d’ajouter des fichiers externes contenant les débits à forcer soit en entrée et/ou en sortie.

Contrairement au sous-bassin, il est attendu que les deux parties de « outFlow », c’est-à-dire « Raw » et « Net », soient différentes en sortie de module anthropique. Concrètement, la variable « outFlowRaw » fera ici référence au trajet naturel du cours d’eau, tandis que « outFlow » modélisera la situation réelle ou celle souhaitée après application des divers interventions humaines en amont.

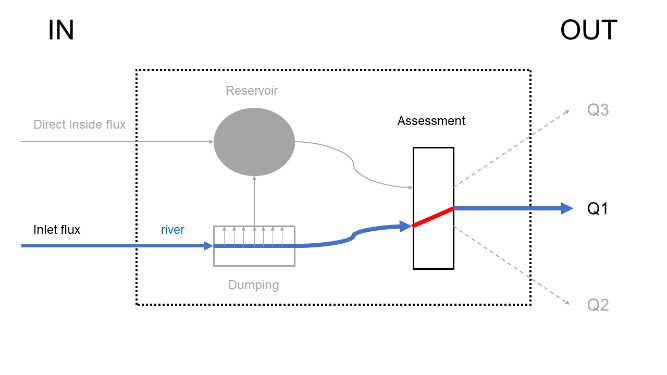
Figure 27 Exemple de rivière naturelle

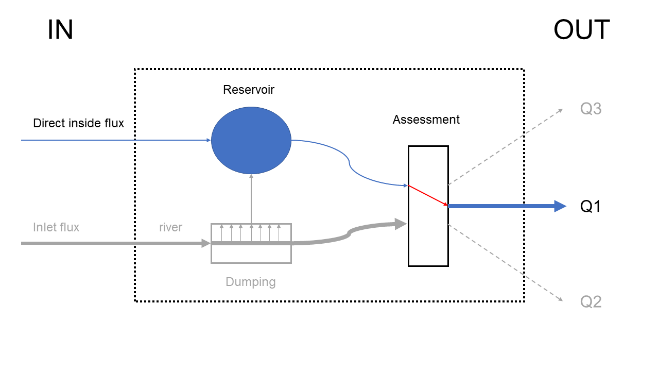
Figure 28 Exemple de barrage

Figure 29 Exemple de dérivation

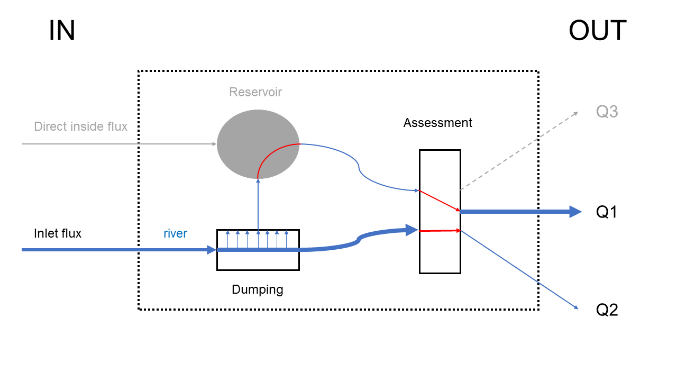
Figure 30 Exemple de bassin d’orage

Divers cas particuliers peuvent être appliqués à cette structure de module pour illustrer son fonctionnement. Dans la Figure 27, ce module est utilisé pour représenter une rivière naturelle. Le réservoir et ses débits rentrants ne seront inutiles et aucun écrêtage n’est nécessaire. Dans le module de bilan, seul le débit en rivière est gardé pour déterminer le débit de sortie. D’autres types de constructions, plus utiles, peuvent être modélisé avec ce module. Un barrage simple, représenté sur la Figure 28, utilise quant à lui uniquement la partie du réservoir de ce module. L’utilisateur pourra donc contrôler le débit de sortie de barrage par une loi de hauteur-débit interne ou personnalisée, ou encore en l’imposant directement. La Figure 29 représente une façon de modéliser une dérivation. Dans le bassin versant de la Vesdre, la Helle est déviée de son cours naturel vers le barrage de la Vesdre de façon à lui fournir un débit maximal de 20 m³/s. et tout surplus est transféré dans la rivière naturelle. Une telle configuration peut être représentée de deux façons. Une première, celle représentée sur la Figure 29, consiste à utiliser la fonction d’écrêtage pour séparer les deux débits. Le flux écrêté sera dévié vers un réservoir de capacité nulle, pour ne plus modifier le flux. Le module de bilan se chargera donc de garder ces deux flux séparés et de considérer le flux provenant du réservoir comme étant le principal (Q1, trajet naturel du cours d’eau vers Eupen) et d’attribuer le débit secondaire au débit artificiel vers le barrage. Une façon alternative de modéliser une dérivation serait de laisser le module de bilan se charger lui-même de séparer les flux en les écrêtant.

Dans le cas d’un bassin d’orage identique à celui présent sur l’Orbais et représenté Figure 30, toutes les composantes peuvent être utilisées. La rivière échange, par exemple par écrêtage, avec le réservoir qui représentera le bassin en lui-même, celui-ci pouvant être rempli par transfert hydrologique des sous-bassins périphériques. Le débit sortant du bassin sera restitué à la rivière via le module de bilan par une simple addition des flux.

Exemple d’adaptation de modèles

La structuration du code en « tiroirs » permet de créer aisément des variantes en couplant des modèles existants : Un exemple de tel modèle original est opérationnel dans WOLF. La structure de celui-ci garde la même forme que le modèle VHM. Les précipitations sont décomposées en trois écoulements différents avec trois différents temps caractéristiques. Mais cette fois, les équations et les procédures inhérentes sont modifiées pour améliorer les performances et la flexibilité.

En première approche, le module de production de VHM est conservé et les changements sont focalisés sur les modules de transfert et, tout particulièrement, sur le ruissellement de surface.

Dans l’écoulement de surface, le réservoir linéaire de la méthode VHM est modifié en considérant deux configurations différentes :

• Dans la première, la cascade de réservoirs linéaires du modèle de Nash est utilisée. Ce nouveau modèle contient 12 paramètres. La motivation derrière ce changement est d’apporter une meilleure représentation du ruissellement afin de prédire avec plus de précision la dynamique de l’hydrogramme total.

• Dans la seconde, le réservoir linéaire de surface est remplacé par un modèle gridded basé sur le recours au nombre de Froude. Ce nouveau modèle contient 15 paramètres. Le but est d’ajouter un peu plus d’informations distribuées dans ce modèle « lumped » et ainsi capter un peu plus les caractéristiques particulières de chaque bassin.

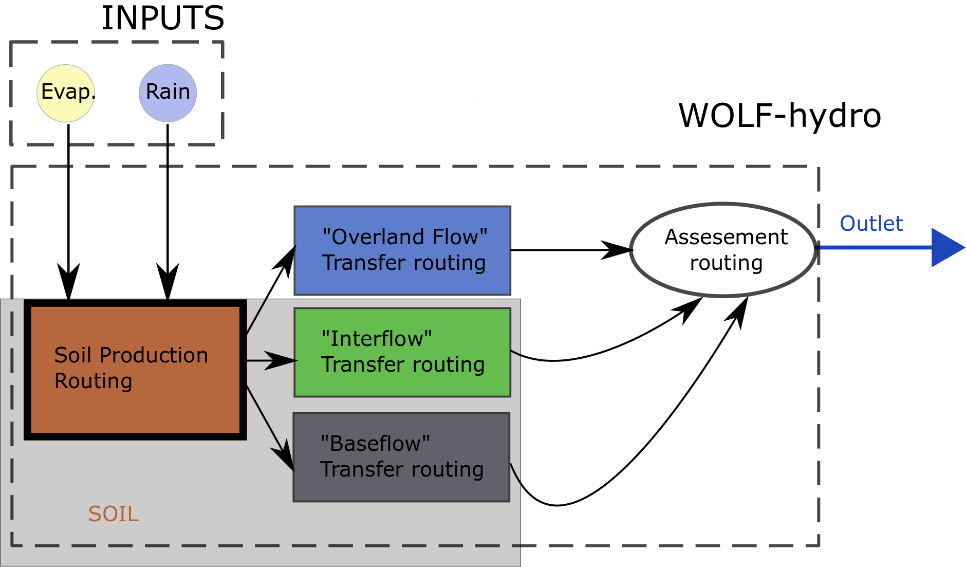
Figure 31 Représentation générale du modèle WOLFHydro

Prétraitement des données d’entrée

Donnés spatialisées

WOLF est capable de lire des données maillées sur base de fichiers « shapefile », GRIB ou encore netCDF.

Les données exploitées avec un « shapefile » seront accompagnées d’un autre fichier apparenté contenant l’évolution au cours du temps pour chaque maille.

Voici quelques exemples de sources exploitables

IRM

L’IRM peut fournir des données journalières de pluie et de température moyenne sur une grille de résolution de 10 km² (exemple de grille à la Figure 32322019). Cette grille peut être lue dans un fichier « shapefile » et les données apparentées dans un fichier « .dbf ». Les pluies peuvent directement être utilisée en entrée des modèles hydrologique tandis que les températures peuvent être exploitées pour calculer l’évapotranspiration (voir Section 7.3) ;

Courbes QDF par municipalité

Contient les fichiers de pluies statistiques pour 12 périodes de retour (2, 5, 10, 15, 20, 25, 30, 40, 50, 75, 100 et 200 ans) et réparties par commune. Les polygones appliqués sont contenus dans des « shapefiles » et peuvent être exploitées dans des études de prédiction événementielle.

Copernicus

Ces données du projet européen Copernicus fournissent des pluies et températures maximales, minimales et moyennes. Elles sont stockées dans des fichiers netCDF.

MAR

MAR est un modèle climatique développé au sein de l’ULiège. Il fournit ses résultats au format netCDF et peut donc servir au forçage d’un modèle WOLFHydro . Cette suite de logiciels est actuellement testée sur des bassins wallons.

Figure 32 Maillage des données IRM sur le BV de l’Ourthe

Données ponctuelles

Les données fournies sont souvent issues de mesures ponctuelles à différentes stations. Voici quelques exemples de données exploitables :

SPW

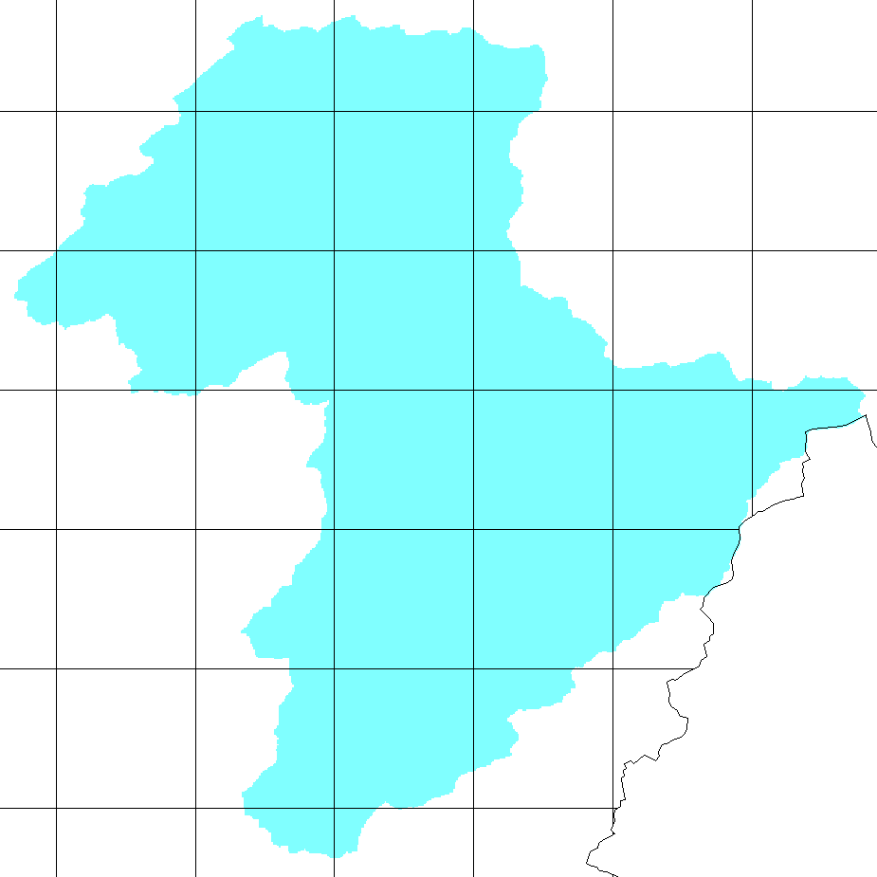
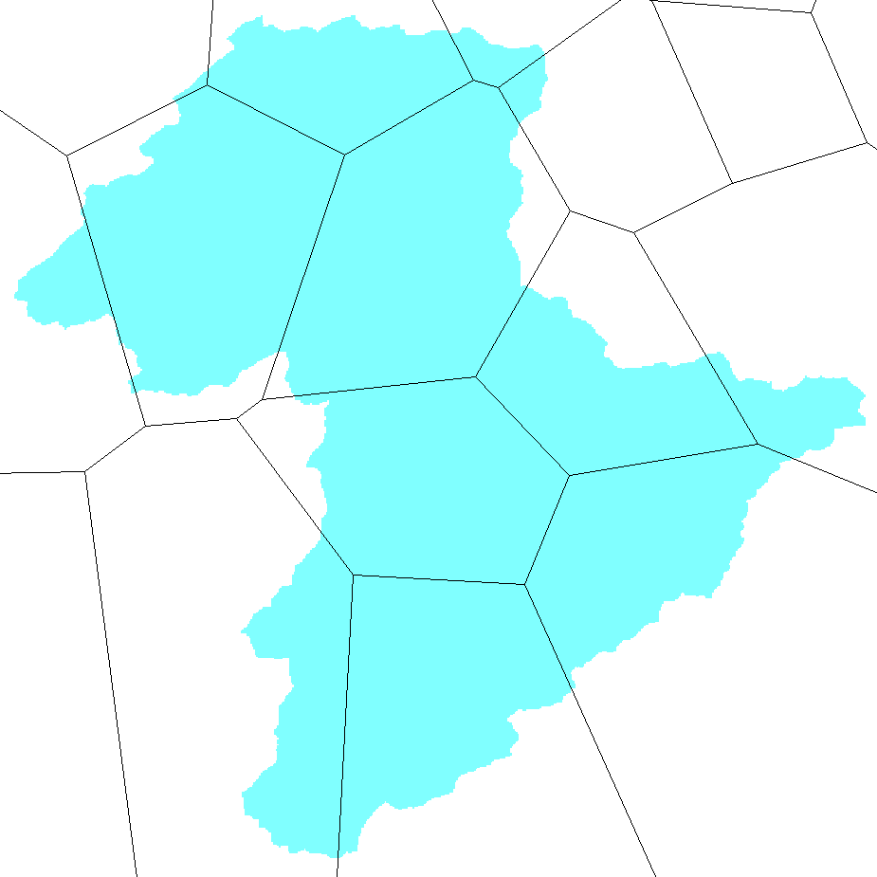
Données de pluies mesurées aux différentes stations fournies par le service public de Wallonie (SPW-MI). Ces données sont ponctuelles et les coordonnées des stations seront fournies en Lambert72. Une procédure de spatialisation est donc appliquée pour attribuer à chaque cellule une donnée de pluie. La méthode choisie par défaut est basée sur la formation de polygones de Thiessen (aussi appelés diagrammes de Voronoï).

Ces polygones garantissent qu’à chaque maille soit attribué les pluies de la station la plus proche. Autrement dit un point à l’intérieur d’un polygone reçoit les pluies de la station entourée par ce polygone. Si une maille hydrologique est intersectée par une arête de ces diagrammes de pluie, alors une moyenne pondérée grâce aux fractions de surface relative à chaque polygone.

Figure 33 Exemple d’une configuration de maillage de pluies SPW sur le bassin de l’Ourthe

Cependant, il existe un certain nombre de contraintes avec ces données. Celles-ci étant des mesures, voici le type de problèmes qui peuvent être rencontrés :

• La date d’entrée en activité de certaines stations peut ne pas coïncider avec l’intervalle étudié lors de la simulation.

• Les données peuvent être incomplètes à certaines stations et donc discontinues. De telles situations peuvent se produire lors de pannes, travaux de maintenance ou renouvellement des outils de mesure.

• Arrêt définitif d’une station de mesure.

Pour toutes les raisons énoncées ci-dessus, le nombre de stations disponibles va varier au cours du temps et avec lui la structure des polygones de Thiessen. Pour pallier ce problème, il a été décidé de subdiviser le temps de simulation par intervalles durant lesquels un même diagramme sera utilisé. Il existe donc au moins autant d’intervalles qu’il y a de configurations de polygones formés.

Trois types de fichiers sont construits et écrits pour structurer ces différentes subdivisions.

• « ind_unique.txt » : contient une matrice avec autant de lignes qu’il y a de configurations et autant de colonne qu’il y a de stations. Les lignes représentent le numéro de la configuration et les colonnes représentent les stations. La variable stockée dans cette matrice est l’indice dans la liste de pluies mesurées à une station auquel commencer pour cette configuration.

• « nb_ind_unique.txt » : vecteur contenant le nombre de pas de temps à considérer pour chaque configuration.

• « unique.txt » : représente le code de la configuration. La valeur stockée est la conversion en entier sur 8 bytes du code binaire dont le premier élément est la première station et sa valeur est égale à 1 si celle-ci est utilisée dans la configuration présente. Cette définition a pour effet de limiter le nombre de stations exploitable à 64 éléments par bassin versant étudié.Dans l’attribution des pluies aux mailles, toutes les configurations sont parcourues dans l’ordre des lignes de la matrice contenue dans le fichier « ind_unique.txt » pour construire progressivement les pluies de bassin.

Attention, actuellement, les différentes configurations ne sont pas parcourues dans l’ordre chronologique ! Cela peut avoir un impact sur l’utilisation de fonction de production qui utilisent une variation de paramètres sur base d’un historique cumulé de précipitations.

Evaluation de l’évapotranspiration

L’évapotranspiration est souvent définie comme étant la quantité d’eau transférée vers l’atmosphère. Une définition précise de phénomène est cependant souvent débattue et peut dépendre de certaines conventions.

Dans le cadre de l’étude hydrologique, l’évapotranspiration de surface est souvent considérée comme étant la fraction du volume de pluie qui ne sera pas considérée dans les différents modèles hydrologiques. Cependant, l’évapotranspiration provenant du sol peut être considérée dans certains modèles. C’est la raison pour laquelle les évapotranspirations calculées dans les méthodes proposées ci-dessous seront plutôt appelées « évapotranspirations potentielles » car il ne s’agit pas d’évapotranspiration réelle, mais plutôt de la partie de l’évapotranspiration avant application du modèle hydrologique et potentiellement de sa modification.

Contrairement aux débits de pluie qui peuvent directement être mesurés, l’évapotranspiration ne peut pas être obtenue directement. Son estimation dépend de la qualité du modèle choisi et des hypothèses qui sont à sa base. Si un modèle inclut l’évapotranspiration en entrée, il est important de garder à l’esprit que cette donnée inclura une certaine incertitude.

Pour évaluer cette donnée, plusieurs techniques ont été implémentées dans WOLF. Celles-ci sont présentées dans les sections ci-dessous.

Oudin2005

Dans cette section, une méthode originale est présentée en appliquant la technique proposée par Oudin2005 à laquelle sont appliqués des coefficients correcteurs par saison.

Les données nécessaires pour appliquer cette méthode sont les données de température maximale et minimale de l’IRM à pas journalier et de discrétisation identique à celle des pluies introduites dans la Section 7.1.1.

Dans l’application de cette méthode pour le bassin versant de l’Ourthe, il apparaît que cette technique surévalue l’évapotranspiration. En tout cas, si le volume total (e.g. avec évaluation un volume cumulé sur une période suffisamment longue) d’évapotranspiration noté $E$ est défini comme suit :

\[E = P - Q\],

avec $P$ le volume de pluies tombées et $Q$ le volume de débits mesurés.

Sur la Figure 34342221, il est possible d’observer que les débits cumulés, appliqués sur le bassin versant l’Ourthe et évalués sur une longue période, sont fortement sous-estimés. Le modèle utilisé dans cette simulation est VHM. Ce modèle vérifie, sur une période suffisamment longue, l’Equation . Les pluies étant des données mesurées, l’hypothèse que celle-ci sont exactes semble raisonnable. Dès lors, les différences entre les volumes cumulés des débits mesurés et simulés peuvent être considérées comme exclusivement engendrées par l’évapotranspiration.

Figure 34 Volumes des débits cumulés avant et après correction sur le bassin de l’Ourthe à Tabreux de 1990 à 2012

Une décomposition plus précise de ces volumes cumulés est obtenue en les séparant par saison. Elle permet d’observer que la technique d’Oudin est surtout bien adaptée pour évaluer l’évapotranspiration en été. Elle échoue cependant complètement à l’évaluer en hiver en la surestimant grandement. Les performances de cette méthode dépendent donc fortement de la saison choisie.

Ce raisonnement suggère de corriger cette méthode en appliquant un coefficient correcteur $\alpha $ à l’évaporation potentielle ${e_p}$ évaluée à chaque pas de temps avec la technique d’Oudin. Dès lors, l’évapotranspiration corrigée ${e_{{\rm{corr}}}}$ à chaque pas de temps devient :

\[{e_{{\rm{corr}}}} = \alpha \;{e_p}\].

Dans le cas du bassin versant de l’Ourthe, les coefficients correctifs $\alpha $ sont estimés dans le Tableau 3.

Season	$\alpha $
Hiver	1/3
Printemps	0.9
Eté	1.0
Automne	0.7

Tableau 3 Valeurs du coefficient correcteur α pour le bassin versant de l’Ourthe à Tabreux

Ces coefficients peuvent cependant être adaptés manuellement afin d’obtenir des coefficients plus adaptés à chaque bassin.

Modèle climatique

MAR_clim

Le modèle climatique MAR développé à l’ULiège par X. Fettweiss est un modèle climatique physiquement basé et distribué.

Les données sont fournies en fichiers de formats netCDF.

La structure générale du modèle est décrite dans la Figure.

Figure 35 Structure du modèle MAR

Le modèle MAR est décomposé en deux parties :

• Un premier module qui calcule les pluies (RF-RainFall) et les neiges (SF-SnowFall) tombées.

• A ces deux premières données va s’appliquer un module de terrain SISVAT. Ce module de terrain est lui-même décomposé en divers sous-modules représentant les différentes couches de sol. A chacune d’elles, deux différents types de flux seront en sortie : une partie ruissellement notée par le préfixe « RO » et une partie rendue à l’atmosphère notée par les préfixes « S » et « E ». Voici le détail des différents sous-modules :

  • module Canopée : représente la couche émergente supérieure des forêts et autres organismes biologiques. Une partie des pluies arrive au sol (RO1) tandis qu’une autre humidifie la canopée et est par la suite évaporée avant d’arriver au sol. En l’absence de canopée $EP = 0$ et $RO1 \approx RF$.

  • module Neige :représente l’accumulation et la fonte des neiges arrivant sur le sol. Ce module prend également en compte l’eau s’accumulant à la surface de couche de glace. Une partie de cette neige est directement ruisselé (si aucune neige $RO2 = 0$) et l’autre fond et arrive au sol (RO3). Le reste est évaporé dans l’atmosphère.

  • module Surface: représente quelle portion de pluie entrera directement dans le sol et quelle portion restera en surface (RO4). La variable RO4 est donc le rapport entre la perméabilité du sol et la diffusivité hydraulique. Une partie de l’eau en surface sera une nouvelle fois évaporé.

  • module Sol : représente les écoulements souterrains sur une couche 10 mètres sous le sol. Il se décompose en 3 flux différents : une partie sera convertie directement en ruissellement si le sol est saturé en eau (RO5), une autre s’infiltrera plus profondément dans le sol avant d’être de refaire surface et transformé en ruissellement, et la dernière transformera l’humidité du sol en évapotranspiration.L’évapotranspiration totale ${e_{{\rm{tot}}}}$ sera donc la somme

\[{e_{{\rm{tot}}}} = EP + ET + SL + SF\].

La conservation de la masse sera respectée à chaque pas de temps en définissant le ruissellement total (RU) avec la relation suivante :

\[RU = RF + SF - (EP + ET + SL + SN)\]

La tâche de WOLFHydro est déjà de modéliser le comportement des pluies arrivant sur le sol et de simuler la façon dont celles-ci seront transmises. Les modules de surface et de sol du modèle MAR sont ainsi redondants avec ceux de WOLF. Le modèle Neige, quant à lui, est clairement un force de MAR.

Dès lors, pour intégrer ce modèle à WOLF, les deux propriétés à extraire sont la pluie effective arrivant au niveau du sol et l’évapotranspiration déjà effectuée avant cette étape.

Concrètement, la pluie effective ${r_i}$ est donnée par la relation

\[{r_i} = \left\{ {\begin{array}{*{20}{l}}

{RO2}&{,{\rm{si module neige dans WOLF}}}\\

{RO3}&{,{\mkern 1mu} {\rm{si aucun module neige dans WOLF}}}

\end{array}} \right.\]

Et l’évapotranspiration potentielle ${e_p}$donnée par les variables

\[{e_p} = \left\{ {\begin{array}{*{20}{l}}

{EP}&{,{\rm{si un module neige dans WOLF}}}\\

{EP + SN}&{,{\mkern 1mu} {\rm{si aucun module neige dans WOLF}}}

\end{array}} \right.\]

Le maillage de toutes les variables citées précédemment pour ce modèle distribué est représenté sur la Figure 36362423.

Figure 36 Maillage des données MAR sur le bassin de l’Ourthe à Tabreux

Calibration

Algorithmes

Dans les sections suivantes, les différentes méthodes d’optimisation implémentées dans WOLF sont décrites. Cependant, il est possible d’ajouter toute autre technique d’optimisation sans calcul de gradient dans la structure actuelle du code.

Screening.

Le « Screening » est une méthode d’optimisation qui consiste à tester toute une liste de paramètres ou configuration de paramètres fournie pour l’utilisateur. Parmi tous ces tests, le meilleur sera gardé en mémoire et considéré comme configuration optimales. Cette méthode ne permet pas de trouver un extremum local. Néanmoins, avec une bonne connaissance a priori de la forme des résultats et un parcours progressif - par exemple sous forme de maillage - d’une précision suffisante, il est possible d’estimer la localisation approximative de l’extrema recherché. C’est la raison pour laquelle cette méthode est souvent combinée avec un algorithme d’optimisation formel pour balayer, au préalable, les possibles concavités et se concentrer par la suite sur la région la plus prometteuse avec l’algorithme formel. De cette manière, on évite à l’algorithme formel d’être prisonnier d’extrema locaux et de rater l’extremum général.

Méthode du Recuit Simulé (Simulated Annealing)

Un module [6] contenant l’algorithme d’optimisation globale du Recuit Simulé continu (en anglais « Simulated Annealing ») est également implémenté dans WOLF comme décrite par Corana et al. [7]. C’est une méthode d’optimisation par inférence Bayésienne qui ambitionne à trouver un extremum global en parcourant aléatoirement de nouvelles valeurs de paramètres se situant dans une certaine fenêtre qui deviendra de plus en plus petite et localisée. Dans cette recherche, chaque nouveau paramètre test fournissant une meilleure fonction objectif sera gardée en mémoire comme optimum temporaire. Cependant, tout jeu de paramètres moins performant ne sera pas systématiquement rejeté et la décision de garder le paramètre dépendra du critère de Métropolis [8]. Dans celui-ci, la température, un paramètre de l’algorithme, et la taille de la fenêtre de recherche seront utilisées d’une manière probabiliste. Ainsi, plus la température de T diminue, plus la fenêtre de recherche rétréci et l’algorithme se concentrera sur la région la plus prometteuse pour l’optimisation.

Fonction objectif

Le choix d’un algorithme d’optimisation le plus performant possible n’est pas suffisant dans la calibration des paramètres. Tout dépend des besoins pour lesquels le modèle doit être utilisé. Un modèle peut très bien être performant pour prédire les crues mais médiocre pour les étiages.

L’idéal serait de reproduire la réalité en toute situation, mais dans le cas d’un modèle conceptuel cette approche serait tout à fait illusoire. C’est pourquoi il est important de définit correctement la fonction objectif en fonction des besoins de l’utilisateur.

Le choix d’un indicateur représentant la qualité d’un résultat n’est pas non plus naturel et particulièrement en Hydrologie.

L’outil le plus populaire en hydrologie est probablement le coefficient de Nash-Sutcliffe (NSE) [9]. Il est défini de la façon suivante :

\[{\rm{NSE}} = 1 - \frac{{\sum\limits_{i = 1}^N {{{(Q_i^s - Q_i^o)}^2}} }}{{\sum\limits_{i = 1}^N {{{(Q_i^o - {{\bar Q}^o})}^2}} }}\],

Où $Q_i^s$ est le ${i^{{\rm{i\`e me}}}}$ élément des débits simulés, $Q_i^p$ est le ${i^{i\`e me}}$ élément des débits observés et ${\bar Q^o}$ le débit moyen observé à partir des $N$éléments.

Un des principaux défauts attribués à cet indicateur est qu’il donne trop d’importance à la précision durant les crues. Une formulation alternative serait de prendre le NSElog défini comme suit

\[{\rm{NSElog}} = 1 - \frac{{\sum\limits_{i = 1}^N {{{[\log (Q_i^s) - \log (Q_i^o)]}^2}} }}{{\sum\limits_{i = 1}^N {{{[\log (Q_i^o) - \log ({{\bar Q}^o})]}^2}} }}\].

Dans ce dernier, l’efficacité du modèle en période d’étiage sera particulièrement mise en lumière.

Cependant pour les deux approches, un léger déphasage entre les données observées et simulées peut entraîner une dégradation significative du nombre de Nash. De plus, cet indicateur fourni peu d’indications concernant qualité de la dynamique des hydrogrammes.

Selon les besoins de l’utilisateur, WOLF laisse la possibilité à celui-ci de calibrer uniquement le modèle sur les périodes de crues ou les périodes d’étiages.

L’utilisateur peut compléter un fichier (« compare.how.param ») qui lui laisse la possibilité de choisir manuellement autant d’intervalles qu’il souhaite utiliser pour calibrer son modèle.

Validation

Dans cette section, la validité des algorithmes proposés sera démontrée. Pour ce faire, deux approches différentes ont été sélectionnées pour trouver les paramètres optimaux d’un modèle GR4H sur le bassin versant de l’Ourthe évalué à Tabreux. Tout d’abord, un screening du coefficient de Nash-Sutcliffe est réalisé pour différents intervalles de paramètres. Par ce moyen, la forme générale de l’extremum est ensuite identifiée pour déterminer si le meilleur coefficient obtenu avec les autres méthodes est bien localisé dans la bonne zone. Dans un deuxième temps, l’optimum obtenu est aussi comparé avec le résultat calculé grâce au code airGR [10].

Pour cette approche, le modèle GR4H est le plus adapté grâce au faible nombre de paramètres qui le compose. En effet, plus le nombre de paramètres est élevé et plus le nombre de solutions optimales potentielles risque d’augmenter. De plus, pour un même nombre $p$ de valeurs à tester pour chaque paramètre, ajouter un élément au nombre de paramètres $n$ aurait multiplié par $p$ le nombre de simulations en suivant la relation ${p^n}$.

Dans ces simulations, le bassin versant de l’Ourthe jusque Tabreux a été pris comme référence et la période étudiée va de 1990 à 2000. Les mesures de pluies aux stations SPW et les températures fournies par l’IRM ont été exploitées comme données d’entrées. L’évapotranspiration a été évaluée avec la formule d’Oudin et en utilisant les coefficients correcteurs décrits dans le Tableau 3. Pour toutes les calibrations, les réservoirs ont été considérés comme initialement vides et le coefficient de Nash (NSE) pris comme fonction objectif.

Concernant le screening, 25 valeurs ont été testées pour chaque paramètre de façon à former une grille de taille uniforme autour de l’intervalle de valeurs souhaité. Les résultats de ces simulations sont affichés à la Figure 37372524 et les paramètres optimaux sont rangés dans le Tableau 4. Sur les graphiques de la Figure 37372524, la forme de la solution est convexe ce qui garantit l’existence d’un extremum local et donc d’un jeu de paramètres optimal. De plus, dans l’intervalle considéré, un seul extremum semble émergé lorsque deux paramètres sont fixés. Bien que cet argument ne soit pas suffisant pour garantir qu’une optimisation formelle ne converge pas vers un optimum local différent de l’optimum général, ce résultat rassure néanmoins en montrant que l’aspect de la fonction objectif n’est pas trop complexe. Ce résultat met aussi en évidence la sensibilité des paramètres vis-à-vis de la fonction objectif et plus particulièrement celles observées aux paramètres X2 et X4 qui semblent plus fortes que les autres paramètres. En effet, ces deux paramètres exercent une influence significative sur le NSE. Le paramètre X2 influence directement les débits échangés et donc l’intensité des pics de crues, tandis que le paramètre X4 provoque un déphasage des hydrogrammes. Comme mentionné dans la Section 8.2, ce sont deux facteurs dégradant considérablement la valeur du NSE.

Figure 37 Résultat du screening pour le modèle GR4H

La simulation réalisée avec la méthode du recuit-simulé fourni des paramètres très semblables à ceux estimés avec la méthode du screening, comme observé dans le Tableau 4. La différence entre les paramètres des deux méthodes est inférieure à la discrétisation choisie lors du screening, c’est-à-dire l’espace entre les paramètres.

	X1	X2	X3	X4	N-S
airGR	92.13	-0.48	214.6	28.31	0.895
Screening	93	-0.4	220	27.6	0.893
SA	90.21	-0.48	214.4	28.31	0.894

Tableau 4 Paramètres optimaux pour différentes méthodes d’optimisation

Pour comparer ces résultats avec ceux d’un code externe, une simulation GR4H a été générée avec le code airGR, en choissant la méthode de calibration Michel [11]. Cet algorithme combine un screening avec un algorithme de « plus grande pente » local. Avec ces paramètres, sont obtenus des paramètres très semblables, voire presque identiques, pour certains. Comme constaté lors du screening, les paramètres X2 et X4 sont très proches vu leurs sensibilités sur les résultats. En revanche, une différence un peu plus nette est observée pour le paramètre X1. Le Nash obtenu est très sensiblement meilleur et car, une fois la bonne zone ciblée, un algorithme d’optimisation formelle trouvera l’extremum de façon exacte.

Finalement, ces différentes approches démontrent la validité des algorithmes implémentés dans WOLF en prouvant que :

• Deux méthodes différentes implémentées dans WOLF convergent vers le même résultat.

• Celles-ci sont également en accord avec la calibration effectuée avec un code externe

Exemple d’application à une portion du bassin de l’Ourthe

Toutes les fonctionnalités du code WOLFHydro ont été présentées dans les sections précédentes. Le but celle-ci est de présenter quelques exemples d’applications réalisées avec ce code. Les exemples ont été choisis pour montrer trois grandes caractéristiques de WOLF :

• Sa capacité à reproduire des résultats réalisés par les créateurs ou spécialistes des modèles implémentés dans WOLF ;

• Sa capacité à améliorer facilement des modèles déjà existants grâce à la grande malléabilité de sa structure par module ;

• Sa capacité à tenir compte de l’évolution spatiale des propriétés d’un bassin.Pour ce faire, les analyses se concentreront sur le bassin versant de l’Ourthe évalué jusque Tabreux.

Ce bassin se situe dans les Ardennes belges et l’Ourthe constitue l’un des affluents de la Meuse. Les caractéristiques principales de ce bassin sont rassemblées dans le Tableau 5.

BV (Tabreux)	Surface	[km²]	1615.0
	Périmètre	[km]	324.4
	Pente moyenne	[%]	7.8
	Indice de Gravelius	[-]	2.27
	Temps de Concentration [3]	[heures]	86h49
Occupation du sol	Forêts	[km²]	727.5
	Prairies	[km²]	427.9
	Cultures	[km²]	352.0
	Urbain	[km²]	102.3
	Eau	[km²]	5.2

Tableau 5 Caractéristiques principales du bassin versant de l’Ourthe évalué à Tabreux

Comparaison avec les résultats d’un workshop hydrologie

Dans le cadre d’une collaboration internationale entre les universités et les instituts visant à trouver un consensus autour du développement des modèles hydrologiques et la façon de les évaluer, un article a été rédigé par de Boer-Euser et al. [12] pour comparer différents modèles existants et leurs performances aussi bien temporelles que spatiales.

L’étude s’est concentrée, tout particulièrement, sur le bassin de l’Ourthe évalué à Tabreux, ainsi que deux de ces composantes principales : l’Ourthe Occidentale (évalué à Ortho) et l’Ourthe Orientale (évalué à Mabompré). Parmi les modèles mis à l’épreuve, VHM et GR4H étaient présents. Plusieurs contraintes étaient imposées aux auteurs de cette études :

• Les données de pluies étaient directement fournies pour l’ensemble du bassin. Ces pluies ont été générées, au préalable, en spatialisant les pluies horaires mesurées aux stations de la SPW (Service Publique de Wallonie) par le moyen de polygones de Thiessen ;

• L’évapotranspiration potentielle était directement fournie pour l’ensemble du bassin. Des données de températures maximales et minimales maillées ont été collectées de la base de données E-OBS auxquelles furent appliquées une fonction sinusoïdale et les données de radiation à Maastricht (KNMI) pour désagréger les données dans un pas horaire. Grâce à ces températures, une évaporation potentielle fut calculée avec la formule de Hargreaves ;

• Les mesures à exploiter sont celles réalisées aux stations de Tabreux, Mabompré et Ortho ;La calibration des modèles doit être réalisée au cours de la période [2004-2007], en utilisant l’année 2003 comme une année de mise en route des modèles. La méthode de calibration était laissée libre aux contributeurs de cette étude leur permettant ainsi d’appliquer librement leur expertise dans le modèle qu’ils se sont vu attribués ;

• 20 réalisations ou résultats d’optimisation étaient demandés pour chaque modèle. Cette information permet d’illustrer la difficulté d’un modèle à être correctement calibré.

Cette section a pour vocation de reproduire les mêmes résultats pour les modèles VHM et GR4H, tout en respectant les mêmes contraintes imposées aux coauteurs du travail. Il est important de mentionner que le modèle GR4H utilisé dans l’étude [12] contient en plus un module Neige, ce qui n’est pas le cas du modèle implémenté dans WOLFHydro . Outre ces deux modèles, seront testés les performances du modèle alternatif de WOLFHydro présenté dans la Section 6 et remplaçant, dans le modèle VHM, le réservoir linéaire de l’écoulement de surface par un modèle de Nash.

Au lieu d’appliquer 20 calibrations pour chaque modèle, le nombre sera réduit à 4. La fonction objectif choisie est le coefficient de Nash-Sutcliffe (NSE) et l’algorithme d’optimisation sera celui du Recuit-Simulé (Section 8.1.2) appliqué à tous les paramètres. Lors de la procédure d’optimisation, les paramètres initiaux seront déterminés aléatoirement. L’approche proposée a l’avantage d’utiliser la même méthode d’optimisation.

	2001-2003 Validation	2004-2007 Calibration	2008-2010 Blind validation
GR4H**	0.93 (0.93-0.93)*	0.89-0.89 (0.89-0.89)*	0.89 (0.88-0.88)*
VHM	0.88 (0.87-0.90)*	0.87-0.88 (0.87-0.88)*	0.86 (0.87-0.88)*
VHM-UH (Nash)	0.89	0.88-0.90	0.89

Tableau 6 NSE à Tabreux et comparaison avec les résultats de l’article de référence [12] (entre parenthèses)

2 001- 2003 Vali dati on 2 004- 2007 C alib rati on 200 8-20 10* B lind vali dati on G R4H* * 0.90 ( 0.82 -0.8 3)* 0 .88- 0.88 ( 0.80 -0.8 1)* 0.85 ( 0.75 -0.7 6)* V HM 0.86 ( 0.88 -0.9 0)* 0 .87- 0.89 ( 0.85 -0.8 6)* 0.85 ( 0.82 -0.8 5)* VH M-UH (Nas h) 0.86 0 .86- 0.88 0.84 Tableau 7 NSE à Ortho et comparaison avec les résultats de l’article de référence [12] (entre parenthèses)

2 001- 2003 Vali dati on 2 004- 2007 C alib rati on 200 8-20 10* B lind vali dati on G R4H* * 0.85 ( 0.82 -0.8 2)* 0 .86- 0.86 ( 0.77 -0.7 8)* 0.75 ( 0.72 -0.7 2)* V HM 0.89 ( 0.84 -0.8 6)* 0 .84- 0.88 ( 0.82 -0.8 5)* 0.81 ( 0.77 -0.8 1)* VH M-UH (Nas h) 0.86 0 .87- 0.88 0.82 Tableau 8 NSE à Mabompré et comparaison avec les résultats de l’article de reference [12] (entre parenthèses)

Une comparaison des différents NSE obtenus avec WOLFHydro est classée dans le Tableau 6, le Tableau 7 et le Tableau 8. Les valeurs indiquées entre parenthèses sont celles obtenues dans l’étude de référence. Pour les colonnes de calibrations, les intervalles de NSE obtenus sont, à chaque fois, retranscrit dans le tableau, mais en ce qui concerne les périodes de validations, seul le meilleur lot de paramètres est utilisé pour déterminer le NSE.

Pour le modèle VHM, il apparait que les Nash obtenus correspondent assez fidèlement aux intervalles obtenus dans l’article. A Ortho, l’intervalle des NSE de WOLFHydro à la calibration semble meilleurs, mais cette amélioration ne se retranscrit pas forcément dans les résultats pour les deux autres intervalles de validation. Bien que le NSE obtenu avec les meilleurs paramètres à la période 2008-2010 sont similaire aux meilleurs paramètres obtenus dans la référence, ceux de la période sont 2001-2003 sont moins bons que tous ceux déterminés dans l’article. En revanche, A Mabompré, un meilleur jeu de paramètres a été trouvé et celui-ci améliore les NSE à tous les intervalles. Bien que la démarche utilisée, par l’auteur des simulations dans l’article, n’est pas explicitée, P. Willems recommandait [2] de d’abord séparer au préalable les hydrogrammes en ses trois différentes couches d’écoulement à l’aide d’un filtre digital et d’ensuite calibrer les constantes de récession des réservoirs linéaires par analyse visuelle des pentes logarithmiques. Cette approche est complètement différente de la nôtre qui consiste à calibrer tous les paramètres à la fois de façon objective et sur seule base du coefficient de Nash-Sutcliffe.

Dans le modèle GR4H, les résultats sont parfaitement identiques à Tabreux. Aux autres stations, WOLFHydro trouve des paramètres qui améliorent systématiquement les NSE calculés. L’absence du module neige dans WOLF-HYDRO peut justifier cette détérioration des résultats pour GR4H-CemaNeige.

A l’instar de VHM, WOLFHydro obtient généralement les NSE les plus stables sur tous les bassins et quelques soit la période considérée. De plus, l’ajout de réservoirs linéaires à la couche superficielle de l’écoulement tend à améliorer globalement la qualité du NSE ainsi que la dynamique des hydrogrammes. Néanmoins, à Ortho, les NSE de WOLFHydro sont inférieurs à VHM, ce qui prouve la difficulté d’un modèle avec autant de paramètres à trouver sa configuration optimale. Pour rappel, la calibration a été entièrement laissée à l’algorithme du Recuit-Simulé sans intervenir aucunement dans un choix plus pertinent pour certains paramètres. Le modèle de WOLFHydro utilisé ici demeure une amélioration de VHM. En effet, dans le pire des cas, il est possible de revenir vers ce dernier en imposant nombre de réservoirs à un et en définissant la même constante de récession.

L’effet d’un changement de technique pour le calcul d’évapotranspiration sur cette étude peut être analysé. Dans WOLFHydro , une procédure alternative a été proposée dans la Section 7.3.1. Pour ce cas d’étude, elle est appliquée en utilisant les températures minimales et maximales journalières fournies par l’IRM auxquels la formule d’Oudin sera employée. Une nouvelle calibration est ainsi menée en gardant toutes les autres données identiques.

Figure 38 Volumes cumulés d’évapotranspiration à Tabreux

Figure 39 Volumes cumulés d’évapotranspiration à Ortho

Figure 40 Volumes cumulés d’évapotranspiration à Mabompré

Une étude comparative des volumes cumulés avec ces différentes méthodes est représentée dans la Figure 38382625, la Figure 39392726et la Figure 1. Dans celle-ci, on distingue que moins d’évapotranspirations ont été estimées dans les données fournies dans l’étude que les celles calculées par WOLF. En revanche, c’est le cas contraire qui est observé à Mabompré.

	2001-2003 Validation	2004-2007 Calibration	2008-2010 Blind validation
GR4H**	0.93	0.88	0.86*
VHM	0.90	0.90	0.88
Wolf-Hydro	0.93	0.91	0.89

Tableau 9 NSE à Tabreux avec calcul de l’évapotranspiration comme présenté

2 001- 2003 Vali dati on 2 004- 2007 C alib rati on 200 8-20 10* B lind vali dati on G R4H* * 0.91 0.80 0. 81* V HM 0.90 0.87 0.85 Wol fHyd ro* 0.90 0.87 0.87 Tableau 10 NSE à Ortho avec calcul de l’évapotranspiration comme présenté

2 001- 2003 Vali dati on 2 004- 2007 C alib rati on 200 8-20 10* B lind vali dati on G R4H* * 0.88 0.85 0. 78* V HM 0.86 0.84 0.80 Wol fHyd ro* 0.87 0.90 0.83 Tableau 11 NSE à Mabompré avec calcul de l’évapotranspiration comme présenté

Les résultats obtenus avec cette nouvelle méthode sont fournis dans le Tableau 9, le Tableau 10 et le Tableau 11. On observe que les performances de tous les modèles sont améliorées pour Ortho et Mabompré. Pour Tabreux, les performances sont améliorées pour VHM et WOLFHydro , mais ce n’est pas le cas de GR4H qui est se voit légèrement moins performant dans l’intervalle de temps 2008-2010. Globalement, le modèle WOLFHydro semble être le meilleur sur tous les bassins versants. Comme dans la configuration précédente, les débits à Mabompré sont de moins bonnes qualités lors de la période 2008-2010.

Finalement, comme dans l’article de de Boer-Euser et al. [12] il peut être conclu que les performances des différents modèles sont relativement identiques en termes de Nash. D’autant plus que la méthode employée pour évaluer l’évapotranspiration une très grande influence sur la hiérarchisation des modèles.

Impact de l’amélioration de WOLFHydro sur un intervalle de temps plus grand

Dans la section précédente, la période de calibration était relativement courte et ne comprenait pas forcément des épisodes météorologiques extrêmes. Cette section s’intéresse à l’effet d’une plus longue période d’entraînement des modèles sur ses performances.

Dans les simulations réalisées, sont considérées en entrée les mêmes données des pluies calculées de façon identique à celle réalisée dans la section précédente, en appliquant des évapotranspirations reconstruites déterminées avec les températures de l’IRM et la formule d’Oudin. La période de simulation s’étendra cette fois-ci de 1990 à 2012 en appliquant la calibration sur l’intervalle 1990-2000.

Dans la procédure de calibration, sont appliqués pour le modèle VHM et le modèle GR4H une première période calibration à partir de valeurs aléatoires permettant d’évaluer un premier jeu de paramètres optimaux. Ceux-ci serviront ensuite de paramètres initiaux lors de trois essais de calibration dans le but de converger plus rapidement vers un potentiel meilleur résultat. La meilleure des trois calibrations est gardée pour l’évaluation de toute la période étudiée. Pour le modèle WOLFHydro , la première calibration considère des paramètres optimaux de VHM en y appliquant qu’un seul bassin linéaire pour l’écoulement de surface et la même constante de récession. Une fois les premiers paramètres initiaux obtenus, est appliquée la même procédure que les autres modèles.

	1990-2000 Ca libration	** 1991-2000**	** 2000-2012**	** 1991-2012**
GR4H	0.895	0.914	0.898	0.894*
VHM				0.878
** WolfHydro**	0.922	0.925-	0.917	0.911

Avec ces résultats, il apparait que le NSE du modèle WOLFHydro est maintenant significativement meilleur que les modèles GR4H et VHM pour toutes les périodes.

Le modèle GR4H est très facile à calibrer. A chacune des trois tentatives de calibration, le même jeu de paramètres était atteint. Ce modèle est le plus performant quand il s’agit de prédire les pics de crues.

Le modèle VHM est plus compliqué à calibrer que le modèle GR4H. Certains paramètres du modèle n’ont que peu d’effets sur le coefficient de Nash. Néanmoins, la fonction objectif atteinte varie très souvent dans un intervalle assez restreint de 0.2 voire 0.4 dans le pire des cas. De plus, selon la période de calibration choisie, il est possible d’observer des configurations de séparation entre la couche de ruissellement et la couche intermédiaire avec des proportions différentes, mais fournissant des NSE relativement équivalents. La dynamique de VHM est en moyenne meilleure que le modèle GR4H, mais ces pics de crues tendent à être systématiquement sous-estimés.

L’adaptation du modèle VHM dans WOLFHydro tend à améliorer encore plus la dynamique des hydrogramme et réussit aussi à améliorer les pics de crues. Cependant, ceux-ci restent toujours sous-estimés. Dès lors, pour observer davantage les effets bénéfiques de ce modèle vis-à-vis des autres, il est important de disposer d’une période de calibration suffisamment longue et riche.

Spatialisation

Figure 41 Bassin de l’Ourthe jusque Tabreux en semi-distribué

Dans la décomposition du bassin versant de l’Ourthe en plusieurs sous-bassins, les exutoires de ceux-ci seront des stations de mesures de débits le long de l’Ourthe. De cette façon, il est possible d’évaluer la qualité des résultats de simulations progressivement d’amont en aval du bassin et identifier, en réalisant pour chacun d’eux une optimisation, l’évolution des paramètres optimaux. Les configurations de chaque bassin sont données dans le Tableau 12.

Pour cette approche, sont exploités le modèle GR4H et le modèle WOLFHydro utilisé lors de l’étude précédente. Les méthodes de calibration et les données utilisées en entrée resteront identiques.

BV ( Tabr eux) Surface [ km ²] 1 615 .02 P erimeter [k m] 32 4.4 Average slope [ %] 7.8 G ravelius index [ -] 2 .27 Cence ntration time [ ho ur s] 86 h49 Lan duse Forest [ km ²] 72 7.5 Meadow [ km ²] 42 7.9 Cultures [ km ²] 35 2.0 Ubran [ km ²] 10 2.3 Water [ km ²] 5.2	BV (Dur buy) Surface [ km ²] 1 223 .85 P erimeter [k m] 30 2.4 Average slope [ %] 7 .38 G ravelius index [ -] 2 .44 Cence ntration time [ ho ur s] 67 h08 Lan duse Forest [ km ²] 55 2.8 Meadow [ km ²] 31 8.3 Cultures [ km ²] 27 4.9 Ubran [ km ²] 7 5.1 Water [ km ²] 2.7
BV (Hot ton) Surface [ km ²] 960 .76 P erimeter [k m] 23 4.6 Average slope [ %] 7 .85 G ravelius index [ -] 2 .14 Cence ntration time [ ho ur s] 53 h27 Lan duse Forest [ km ²] 44 9.4 Meadow [ km ²] 23 6.6 Cultures [ km ²] 22 5.2 Ubran [ km ²] 46 Water [ km ²] 2.7	BV (Ni sram ont) Surface [ km ²] 738 .28 P erimeter [k m] 20 9.0 Average slope [ %] 6 .64 G ravelius index [ -] 2 .17 Cence ntration time [ ho ur s] 27 h20 Lan duse Forest [ km ²] 31 4.9 Meadow [ km ²] 18 8.0 Cultures [ km ²] 197 .26 Ubran [ km ²] 3 5.4 Water [ km ²] 2.7
BV (Mabo mpré) Surface [ km ²] 319 .02 P erimeter [k m] 12 2.6 Average slope [ %] 6 .68 G ravelius index [ -] 1 .94 Cence ntration time [ ho ur s] 15 h52 La nduse Forest [ km ²] 14 4.4 Meadow [ km ²] 8 2.6 Cultures [ km ²] 7 3.3 Ubran [ km ²] 1 6.3 Water [ km ²] 0	BV (Or tho) Surface [ km ²] 386 .08 P erimeter [k m] 12 3.8 Average slope [ %] 6 .17 G ravelius index [ -] 1 .78 Cence ntration time [ ho ur s] 18 h39 Lan duse Forest [ km ²] 15 2.6 Meadow [ km ²] 10 0.9 Cultures [ km ²] 11 4.6 Ubran [ km ²] 1 7.9 Water [ km ²] 0

Tableau 12 Caractéristiques principales de tous les sous-bassins évalués aux stations de mesures de débits sur l’Ourthe en amont de Tabreux ;

Param eters	Tabr eux*	Dur buy	Ho tton	N isramont	** Mabompré**	Or tho
:ma th:ma thbf{X} _{math bf{1}} [mm]	90.21	91.75	88.08	92.19	96.37	79.23
:ma th:ma thbf{X} _{math bf{2}} [mm]	-0.48	-0.5	-0.21	-0.07	-0.67	-0.27
:ma th:ma thbf{X} _{math bf{3}} [mm]	214.4	255.4	287.5	316.51	291.8	352.9
:ma th:ma thbf{X} _{math bf{4}} [h]	28.31	24.0	20.87	13.22	12.17	11.17
N-S	0.894	0.899	0.886	0.878	0.842	0.884

Param eters	Tabr eux*	Dur buy	Ho tton	Ni sramont	M abompré	Or tho
:mat h:mat hbf{k}_ {mathb f{BF}} [h]	1 151.7	1 022.3	737.01	855.79	802.0	9 14.32
:mat h:mat hbf{k}_ {mathb f{IF}} [h]	1 29.65	1 33.68	129.65	121.17	131.0	1 47.89
math: mathb f{U}_{mathbf{ max}} [mm]	1 36.35	1 23.72	255.52	161.34	103.64	1 20.52
:math :`math bf{e}_{ mathbf {evap}} `[mm]	4.05	11.13	2.8	21.53	47.20	4.711
:mat h:mat hbf{a}_ {mathb f{u}ma thbf{1} }[-]	2.069	2.135	3.349	2.0824	0.868	2.715
math: mathb f{a}_{mathbf{ u}math bf{2}} [-]	5.775	5.009	10.0	9.0356	-0.178	1.533
math: mathb f{a}_{mathbf{ u}math bf{3}} [-]	2.719	3.865	2.09	3.583	-18.11	1.364
:math:` mathbf {a}_{m athbf{O F}math bf{1}}` [-]	46.40	51.82	-21.86	-40.0	-66.42	30.25
:math:` mathbf {a}_{m athbf{O F}math bf{2}}` [-]	98.22	82.82	67.60	77.58	65.74	40.22
:math:` mathbf {a}_{m athbf{I F}math bf{1}}` [-]	6.037	19.78	-23.71	-22.28	-7.209	10.68
:math:` mathbf {a}_{m athbf{I F}math bf{2}}` [-]	11.11	31.40	75.61	44.25	6.393	13.84
:mat h:mat hbf{n} [-]	4.34	4.81	3.674	3.88	2.031	2.09
math: mathb f{t}_{mathbf{ peak}} [h]	31.11	30.48	27.73	18.46	16.60	15.27
Cali bration	0.922	0.922	0.915	0.913	0.882	0.907
N-S (199 1-2000)	0.925	0.929	0.922	0.921	0.892	0.922
N-S (200 0-2012)	0.917	0.923	0.916	0.916	0.887	0.919
N-S (199 1-2012)	0.911	0.915	0.904	0.901	0.871	0.903

A chaque station, les tendances observées à la section précédente sur les performances des modèles sont conservées. Le modèle WOLFHydro est meilleur en termes de NSE et de dynamique, tandis que le modèle GR4H estime mieux les pics de crues. Pour les deux modèles, une dégradation du Nash est présente à Mabompré par rapport aux autres sous-bassins.

En analysant en détail l’évolution des paramètres du modèle GR4H, on observe tout d’abord une diminution progressive, de l’aval vers l’amont, de la constante X4. Cette constatation était tout à fait attendue, vu que cette variable représente le temps caractéristique de hydrogrammes unitaires. En d’autres mots, le temps de déphasage entre la pluie et le débit mesuré dépendra presque directement de ce paramètre. Sa valeur se dès lors fonction de la taille du sous-bassin considérer et pourrait aussi être relié au temps de concentration du sous-bassin.

En réalisant la même analyse pour les paramètres optimaux de WOLFHydro , on constate également que la variable ${t_{{\rm{peak}}}}$est aussi fonction de la taille du bassin versant considéré. En effet le pic de crue est lui-même dépendant du temps de concentration et relativement proche du paramètre X4 du modèle GR4H. Le nombre de réservoirs linéaires à appliquer au ruissellement diminue lui aussi avec la surface du bassin forçant l’hydrogramme unitaire de Nash à s’étaler de plus en plus en aval. Cependant, les constantes de récession de l’écoulement intermédiaire ${k_{IF}}$ et de l’écoulement de base ${k_{BF}}$ ne semblent pas être influencées par la taille du bassin.

Si des paramètres identiques à ceux obtenus à Tabreux étaient appliqués à chaque sous-bassin, le Nash obtenus serait progressivement dégradé au fur et à mesure qu’on remonte les bassins versants vers l’amont (de l’ordre de 0.1 en moins pour le NSE à Ortho et Mabompré). A la suite de ces constatations, on pourrait penser que la variabilité spatiale des paramètres est surtout influencée par les variables dépendantes de la taille du bassin versant (X4 pour GR4H ; $n$ et ${t_{{\rm{peak}}}}$pour WOLFHydro). Cependant, si ces paramètres restent inchangés et que les autres paramètres optimaux à Tabreux sont, cette fois-ci, appliqués à l’ensemble des sous-bassins, on n’observe que peu d’amélioration (de l’ordre de 0.03 en plus pour le NSE à Ortho et Mabompré). On peut donc on conclure que la taille du domaine, et les variables y étant liées, ne sont pas les acteurs principaux dans la variabilité spatiale des paramètres.

Interface graphique

Choix de langage

Historiquement, les développements graphiques de la suite logicielle WOLF ont été réalisés en Visual Basic 6. De nombreux outils existent sous cette forme et, malgré le fait que le langage ne soit plus officiellement supporté, sont toujours pleinement fonctionnels.

Cependant, il est nécessaire de faire évoluer les outils vers des solutions plus pérennes. Dès lors, après analyse approfondie des possibilités, les choix posés pour les nouveaux développements de l’interface graphique de WOLF sont les suivants :

• Langages de programmation : Python 3.9 ou ultérieur et OpenGLWidgets WX [4] et plus spécifiquement son portage sous Python [5]

Figure 42 Exemple d’une fenêtre graphique permettant de visualiser les données spatiales du modèle hydrologique

Ces choix rendent normalement l’interface graphique indépendante du système d’exploitation, « cross-platform GUI », tout en assurant une qualité graphique propre à chaque OS.

Pour l’affichage de données matricielles, le recours aux instructions OpenGL permet de bénéficier de la puissance de la carte graphique même pour des visualisation 2D.

Le langage Python rend également accessible une panoplie de librairies open source additionnelles. Parmi celles-ci, sont utilisées dans les développements actuels : Numpy, Matplotlib, Pandas, Scipy, Owslib, Pillow, Dbfread, Graphviz, Owslib, Requests, Notebook, Beautifoulsoup4, Typing, Ctypes…

Finalement, les outils Python de WOLF sont accessibles via un paquet spécifique [6] « wolfhece » disponible sur Pypi.org, ce qui facilite grandement le déploiement et les mises à jour.

Interaction code de calcul

Le langage Python est un langage interprété pour lequel l’efficacité de calcul n’est pas une priorité. Parmi les nombreuses techniques possibles pour remédier à ce problème, le choix d’une interaction avec un code Fortran compilé a semblé une évidence compte-tenu de l’historique de WOLF.

Ainsi, une librairie Python compilée avec l’outil f2py [7] permet l’interaction de scripts et de routines de calcul plus consommatrices en temps. Cette librairie doit toutefois continuer à se développer pour permettre une interaction complète, notamment afin de fournir une porte vers les paramètres à optimiser des codes de calcul pour que des outils externes puissent être exploités et étendre la gamme des techniques actuellement programmées en Fortran.

Dans la même idée de flexibilité, le recours à des fonctionnalités de callbacks permettant les interactions Python🡪Fotran ou Fortran🡪Python et même le partage d’espaces mémoires est possible grâce à l’emploi d’une librairie dynamique DLL et de la librairie Python CTypes. Cette approche est plus générale que l’utilisation de f2py et vient donc la compléter.

Figure 43 Exemple d’une fenêtre graphique permettant de superposer la discrétisation en sous-bassins versant avec les PPNC obtenus via le webservice de Walonmap

Gestion des données

En l’état, l’interface graphique Python actuelle permet d’afficher des informations :

• matricielles en fausses couleurs (topographie, index de bassin versant, accumulation…)

• vectorielles (contours, réseau hydrographique…)

• ponctuelles (stations de mesures, exutoires locaux…)

• extraites via des webservices WMS (Walonmap – orthophotoplans, réseau aqualim, IGN Français…)

Toutes ces données peuvent être combinées.

Figure 44 Exemple d’une fenêtre graphique permettant de superposer la discrétisation en sous-bassins versant avec les stations de mesures SPW et le réseau hydrographique discrétisé

Il ne s’agit pas d’un SIG étant donné que le système de référence est fixe (Lambert72 par défaut pour la Belgique). Le cas échéant, des conversions de système sont possibles au travers de l’outil GDAL.

Figure 45 Exemple de visualisation des profils en long du réseau hydrographique identifié autoimatiquement

Figure 46 Exemple de visualisation des données d’une station de mesures – relation hauteur-débit

Fichier « .hyeto »

Il s’agit d’un fichier, au format ANSI, de pluies pour la période simulée.

La première ligne contient le nombre de valeurs utiles. Les lignes suivantes reprennent sur 2 colonnes :

• Le timestamp Unix en [s]La pluie en [m/s]

• Le pas de temps utilisé est celui du fichier de paramètres de la simulation.

La spatialisation de la pluie stockées dans les fichiers « .hyeto » est fournie via un ESRI Shapefile contenant des polygones. La table attributaire contient le nom de fichier sans extension associé à chaque polygone.

Fichier « .rain »

Il s’agit d’un fichier, au format ANSI, de pluies pour une période plus importante ou égale à la période simulée.

Les quatre premières lignes contiennent :

1. Name : Un nom qui est par défaut le même que le nom de fichier sans extension [string] 2. NbVals : Le nombre de valeurs utiles [integer] 3. NbCols : Le nombre total de colonnes [integer] 4. NbRows : Le nombre de lignes de valeurs

Les lignes suivantes contiennent dans les NbCols colonnes :

• la date

• l’heure

• les valeurs utiles.

La date et l’heure sont codées sur (NbCols-NbVals) colonnes. Si ce calcul donne 3, il n’y a que la date à exploiter, l’heure est supposée nulle. Si le calcul donne 4, 5 ou 6, l’heure est fournie avec une précision différente. Les valeurs non présentes étant supposées nulles.

Par défaut, une intensité de pluie à la date du 02/01/2021 02:00:00 à pas horaire est la quantité de pluie tombée sur l’intervalle ]02/01/2021 01:00:00 ; 02/01/2021 02:00:00]. D’autres interprétations sont néanmoins possibles (centré, décalage à droite et non à gauche vis-à-vis du temps de référence). Cela dépendra en pratique des paramètres de la simulation.

La spatialisation de la pluie stockées dans les fichiers « .rain » est fournie via un ESRI Shapefile contenant des polygones. La table attributaire contient le nom de fichier sans extension associé à chaque polygone.

Références

[1] J. E. Nash, “The form of the instantaneous unit hydrograph,” 1957.

[2] P. Willems, “Parsimonious rainfall-runoff model construction supported by time series processing and validation of hydrological extremes - Part 1: Step-wise model-structure identification and calibration approach,” J. Hydrol., vol. 510, pp. 578–590, 2014, doi: 10.1016/j.jhydrol.2014.01.017.

[3] T. G. Chapman, “Comment on ‘Evaluation of automated techniques for base flow and recession analyses’ by R. J. Nathan and T. A. McMahon,” Water Resour. Res., vol. 27, no. 7, pp. 1783–1784, 1991, doi: 10.1029/91WR01007.

[4] C. Perrin, C. Michel, and V. Andréassian, “Improvement of a parsimonious model for streamflow simulation,” J. Hydrol., vol. 279, no. 1–4, pp. 275–289, 2003, doi: 10.1016/S0022-1694(03)00225-7.

[5] T. Mathevet, “Quels Modèles Pluie-Debit Globaux au pas de temps horaire ? Développements Empiriques et Comparaison de modèles sur un large échantillon de Bassins Versants,” Ecole Nationale du Génie Rural, des Eaux et Forêts, 2005.

[6] “Netlib.” https://www.netlib.org/.

[7] A. Corana, M. Marchesi, C. Martini, and S. Ridella, “Minimizing Multimodal Functions of Continuous Variables with the ‘Simulated Annealing’ Algorithm,” ACM Trans. Math. Softw., vol. 13, no. 3, pp. 262–280, 1987, doi: 10.1145/29380.29864.

[8] N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller, “Equation of state calculations by fast computing machines,” J. Chem. Phys., vol. 21, no. 6, pp. 1087–1092, 1953, doi: 10.1063/1.1699114.

[9] J. E. Nash and J. V. Sutcliffe, “River flow forecasting through conceptual models part I — A discussion of principles,” J. Hydrol., vol. 10, no. 3, pp. 282–290, Apr. 1970, doi: 10.1016/0022-1694(70)90255-6.

[10] L. Coron, G. Thirel, O. Delaigue, C. Perrin, and V. Andréassian, “The suite of lumped GR hydrological models in an R package,” Environ. Model. Softw., vol. 94, pp. 166–171, 2017, doi: 10.1016/j.envsoft.2017.05.002.

[11] C. Michel, Hydrologie appliquée aux petits bassins ruraux, Cemagref Antony. 1989.

[12] T. De Boer-Euser et al., “Looking beyond general metrics for model comparison – Lessons from an international model intercomparison study,” Hydrol. Earth Syst. Sci., vol. 21, no. 1, pp. 423–440, 2017, doi: 10.5194/hess-21-423-2017.

[13] A. F. Van Loon, “Hydrological drought explained,” WIREs Water, vol. 2, no. 4, pp. 359–392, 2015, doi: 10.1002/wat2.1085.

[14] R. J. Nathan and T. A. McMahon, “Evaluation of automated techniques for base flow and recession analyses,” Water Resour. Res., vol. 26, no. 7, pp. 1465–1473, 1990, doi: 10.1029/WR026i007p01465.

[15] M. Le Mesnil, R. Moussa, J. B. Charlier, and Y. Caballero, “Impact of karst areas on runoff generation, lateral flow and interbasin groundwater flow at the storm-event timescale,” Hydrol. Earth Syst. Sci., vol. 25, no. 3, pp. 1259–1282, 2021, doi: 10.5194/hess-25-1259-2021.

[16] C. C. Brauer, P. J. J. F. Torfs, A. J. Teuling, and R. Uijlenhoet, “The Wageningen Lowland Runoff Simulator (WALRUS): Application to the Hupsel Brook catchment and the Cabauw polder,” Hydrol. Earth Syst. Sci., vol. 18, no. 10, pp. 4007–4028, 2014, doi: 10.5194/hess-18-4007-2014.

[17] B. R. Thapa, H. Ishidaira, V. P. Pandey, and N. M. Shakya, “A multi-model approach for analyzing water balance dynamics in Kathmandu Valley, Nepal,” J. Hydrol. Reg. Stud., vol. 9, pp. 149–162, 2017, doi: 10.1016/j.ejrh.2016.12.080.

[18] Y. F. Sang, “A review on the applications of wavelet transform in hydrology time series analysis,” Atmos. Res., vol. 122, pp. 8–15, 2013, doi: 10.1016/j.atmosres.2012.11.003.

[19] M. P. Clark et al., “Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models,” Water Resour. Res., vol. 44, no. 12, pp. 1–14, 2008, doi: 10.1029/2007wr006735.

[20] S. Kumar Singh and N. Marcy, “Comparison of Simple and Complex Hydrological Models for Predicting Catchment Discharge Under Climate Change,” AIMS Geosci., vol. 3, no. 3, pp. 467–497, 2017, doi: 10.3934/geosci.2017.3.467.

[21] Q. Q. Tran, P. Willems, and M. Huysmans, “Coupling catchment runoff models to groundwater flow models in a multi-model ensemble approach for improved prediction of groundwater recharge, hydraulic heads and river discharge,” Hydrogeol. J., vol. 27, no. 8, pp. 3043–3061, 2019, doi: 10.1007/s10040-019-02018-8.

[22] K. Du, Y. Zhao, and J. Lei, “The incorrect usage of singular spectral analysis and discrete wavelet transform in hybrid models to predict hydrological time series,” J. Hydrol., vol. 552, pp. 44–51, 2017, doi: 10.1016/j.jhydrol.2017.06.019.

[23] V. Wolfs, Q. T. Quoc, and P. Willems, “A flexible and efficient multi-model framework in support of water management,” IAHS-AISH Proc. Reports, vol. 373, pp. 1–6, 2016, doi: 10.5194/piahs-373-1-2016.

[24] H. H. G. Savenije, “HESS opinions ‘topography driven conceptual modelling (FLEX-Topo),’” Hydrol. Earth Syst. Sci., vol. 14, no. 12, pp. 2681–2692, 2010, doi: 10.5194/hess-14-2681-2010.

[25] C. Torrence and G. P. Compo, “Wavelet-Guide,” Bull. Am. Meteorol. Soc., vol. 79, no. 1, pp. 61–78, 1995.

[26] R. A Lane et al., “Benchmarking the predictive capability of hydrological models for river flow and flood peak predictions across over 1000 catchments in Great Britain,” Hydrol. Earth Syst. Sci., vol. 23, no. 10, pp. 4011–4032, 2019, doi: 10.5194/hess-23-4011-2019.

[27] C. P. White, “On the use of the term ‘blastoma.,’” Br. Med. J., vol. 1, no. 2163, p. 1514, 1902, doi: 10.1136/bmj.1.2163.1514.

[28] D. Kavetski and F. Fenicia, “Elements of a flexible approach for conceptual hydrological modeling: 2. Application and experimental insights,” Water Resour. Res., vol. 47, no. 11, pp. 1–19, 2011, doi: 10.1029/2011WR010748.

[29] A. K. Mishra and V. P. Singh, “Drought modeling - A review,” J. Hydrol., vol. 403, no. 1–2, pp. 157–175, 2011, doi: 10.1016/j.jhydrol.2011.03.049.

[30] M. I. Brunner, L. Slater, L. M. Tallaksen, and M. Clark, “Challenges in modeling and predicting floods and droughts: A review,” Wiley Interdiscip. Rev. Water, vol. 8, no. 3, pp. 1–32, 2021, doi: 10.1002/wat2.1520.

[31] R. V Galkate, R. K. Jaiswal, T. Thomas, and T. R. Nayak, “Rainfall Runoff Modeling Using Conceptual NAM Model,” 3rd Int. Conf. Sustain. Manag. Strateg. Nagpur Inst. Manag. Technol., p. March, 21-22, 2014.

[32] J. De Niel et al., “Observations : discharge , precipitation and temperature,” 2008.

[33] N. Editor, C. S. Editor, S. Editor, B. Editor, P. Editors, and T. S. Editor, “Mike 11 mike 11,” pp. 1–20, 2020.

[34] P. Willems, D. Mora, T. Vansteenkiste, M. T. Taye, and N. Van Steenbergen, “Parsimonious rainfall-runoff model construction supported by time series processing and validation of hydrological extremes - Part 2: Intercomparison of models and calibration approaches,” J. Hydrol., vol. 510, no. February, pp. 591–609, 2014, doi: 10.1016/j.jhydrol.2014.01.028.

[35] M. Hrachowitz and M. P. Clark, “HESS Opinions: The complementary merits of competing modelling philosophies in hydrology,” Hydrol. Earth Syst. Sci., vol. 21, no. 8, pp. 3953–3973, 2017, doi: 10.5194/hess-21-3953-2017.

[36] C. C. Brauer, A. J. Teuling, P. J. J. F. Torfs, and R. Uijlenhoet, “The Wageningen Lowland Runoff Simulator (WALRUS): A lumped rainfall-runoff model for catchments with shallow groundwater,” Geosci. Model Dev., vol. 7, no. 5, pp. 2313–2332, 2014, doi: 10.5194/gmd-7-2313-2014.

[37] A. Mayssara A. Abo Hassanin Supervised, “済無No Title No Title No Title,” Paper Knowledge . Toward a Media History of Documents, 2014. .

[38] L. J. E. Bouaziz, “Supplement of Behind the scenes of streamflow model performance,” pp. 0–3, 2021.

[39] L. Bouaziz et al., “Behind the scenes of streamflow model performance,” Hydrol. Earth Syst. Sci. Discuss., pp. 1–38, 2020, doi: 10.5194/hess-2020-176.

[40] C. Runoff, M. For, and H. O. C. H. Oceanografi, “Development and application of a conceptual runoff model for scandinavian catchments,” vol. 7, 1976.

[41] C. Brauer, “Modelling rainfall-runoff processes in lowland catchments.”

[42] B. Schaefli and E. Zehe, “Hydrological model performance and parameter estimation in the wavelet-domain,” Hydrol. Earth Syst. Sci., vol. 13, no. 10, pp. 1921–1936, 2009, doi: 10.5194/hess-13-1921-2009.

[2]

Martz and al. https://onlinelibrary.wiley.com/doi/pdf/10.1002/(SICI)1099-1085(199805)12:6%3C843::AID-HYP658%3E3.0.CO;2-R

[3]

Le temps de concentration est celui déterminé par une méthode de Froude

[4]

https://www.wxwidgets.org/

[5]

https://www.wxpython.org/

[6]

https://pypi.org/project/wolfhece/

[7]

https://numpy.org/doc/stable/f2py/