Creating a 2D Simulation with CPU model with turbulence via script

To create a 2D simulation, you need to:

1. Set simulation name and working directory and check .cli model availability

2. Create a new 2D simulation as an instance of prev_sim2D

3. Define the problem geometry (mesh resolution, channel dimensions) and boundary conditions

4. Define a vectorial contour/polygon to outline the working area and add blocks (obstacles)

5. Define a magnetic grid, set the contour, and create the mesh

6. Set the simulation parameters

7. Get boundary cells and set boundary conditions

8. Define initial conditions and other simulation parameters (topography, water depth, friction)

9. Final checks and save the simulation

10. Run the simulation run_wolfcli

And…

1. Access the results

2. Visualize the results

3. Generate an animation

Preliminary steps

Import modules

# general modules
# import _add_path # for debugging purpose - set the right directory - but can be removed in production
import os

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

from pathlib import Path
from IPython.display import HTML, Image

from datetime import datetime as dt
from datetime import timezone as tz
from datetime import timedelta as td

# WOLF modules
from wolfhece.mesh2d.wolf2dprev import prev_sim2D
from wolfhece.PyVertexvectors import vector, wolfvertex
from wolfhece.wolf_array import WolfArray, WolfArrayMB, header_wolf
from wolfhece.mesh2d.cst_2D_boundary_conditions import BCType_2D
from wolfhece.wolfresults_2D import Wolfresults_2D
from wolfhece.wolfresults_2D import views_2D, getkeyblock

Set simulation name and directory

simulation_name = 'tutorial_2D'
curdir = Path(os.getcwd())
print(f'Current directory: {curdir}')

Current directory: d:\ProgrammationGitLab\HECEPython\Floating_Debris\WOLF_simulations

outdir = curdir / simulation_name
outdir.mkdir(exist_ok=True) # create output folder
print(f'Simulation path: {outdir}; name: {outdir.name}')

Simulation path: d:\ProgrammationGitLab\HECEPython\Floating_Debris\WOLF_simulations\tutorial_2D; name: tutorial_2D

Check code availability

Return full path to the executable. It is recommended to have the executable in the directory where this notebook is stored.

wolfcli = prev_sim2D.check_wolfcli() # check if wolfcli is present in the current directory

if wolfcli:
    print('Code found: ', wolfcli)
else:
    print('Code not found!')

Code found:  wolfcli.exe

Create new 2D simulation

Set the working directory by adding the generic simulation name and provide it as ipnut for generating the simulation.

clear=True allows you to delete the files from the previous simulation, if existing.

A message of type logging.warning is emitted because no file was found. This is normal, as you just created the simulation!

If a file is found, this is loaded.

new_dir = outdir / f'{simulation_name}'
newsim = prev_sim2D(fname=new_dir, clear=True)

WARNING:root:No infiltration file found

Define problem geometry and boundary conditions

Definition Method

A polygon/outer contour of the domain to be modeled must be defined.

This is done by creating a “vector” object and encoding its coordinates using a “vector” class – see wolfhece.PyVertexvectors and its tutorial.

Channel configuration:

Geometry

Specify the mesh size (dx, dy), coordinates of the origin (origx, origy), channel dimensions (Lx, Ly), and slope.

dx, dy = 0.01, 0.01 # m
origx, origy = 0., 0. # m
Lx, Ly = 10., 0.6 # m
slope = 0. # m/m

Boundary conditions

Specify the upstream unit discharge (Qx_ups, assuming the flow is directed only in the x-direction at the upstream boundary) and the downstream water depth (h_dws).

Qx_ups = 18e-3 # m2/s
h_dws = 5.8e-2 # m

Define vectorial contour and blocks (obstacles)

Obstacles

Obstacles are defined starting from the bottom-left corner. The width, height, and horizontal spacing among these are additional required parameters.

All corners of the obstacles need to be specified.

n_obs = 3 # number of obstacles per side
spacing_obs = 2. # horizontal spacing between obstacles on each side
width_obs, height_obs = 0.15, 0.12 # width (x) and height (y) of the obstacles

x0up_obs  = 1. # bottom-left x-coordinate of the first obstacle on the upper side
x0low_obs = 2. # bottom-left x-coordinate of the first obstacle on the lower side

# generate bottom-left x-coordinates of the obstacles
x_low_obs = [x0low_obs + i * spacing_obs for i in range(n_obs)] # starting from the left - low side
x_up_obs  = [x0up_obs  + i * spacing_obs for i in range(n_obs)]  # starting from the left - up side

Create a polygon around the domain incorporating the obstacles (add a vertex for all corners of the channel and all corners of the obstacles) by specifying the (x, y) coordinates in the add_vertex function.

contour = vector(name='contour') # create the contour vector

contour.add_vertex(wolfvertex(x=origx, y=origy)) # add origin = bottom-left corner

# add obstacles on the lower side
for i in range(n_obs):
    x = x_low_obs[i]
    y = origy
    # add all vertices of the obstacle
    contour.add_vertex(wolfvertex(x=x, y=y))
    contour.add_vertex(wolfvertex(x=x, y=y + height_obs))
    contour.add_vertex(wolfvertex(x=x + width_obs, y=y + height_obs))
    contour.add_vertex(wolfvertex(x=x + width_obs, y=y))
    # no need to close the obstacle -- just pass to the next one

contour.add_vertex(wolfvertex(x=origx + Lx, y=origy)) # add bottom-right corner
contour.add_vertex(wolfvertex(x=origx + Lx, y=origy + Ly)) # add top-right corner

# add obstacles on the upper side - in reverse order
x_up_obs.reverse() # reverse the list to have the obstacles in the right order
for i in range(n_obs):
    x = x_up_obs[i]
    y = origy + Ly
    # add all vertices of the obstacle
    contour.add_vertex(wolfvertex(x=x + width_obs, y=y))
    contour.add_vertex(wolfvertex(x=x + width_obs, y=y - height_obs))
    contour.add_vertex(wolfvertex(x=x, y=y - height_obs))
    contour.add_vertex(wolfvertex(x=x, y=y))
    # no need to close the obstacle -- just pass to the next one

contour.add_vertex(wolfvertex(x=origx, y=origy + Ly)) # top-left corner
contour.force_to_close() # force the vector to be closed

Visualize the contour

fig, ax = plt.subplots(figsize=(10, 18))
contour.plot_matplotlib(ax)
ax.set_aspect('equal')

Define a magnetic grid, set the contour, and create the mesh

# force the vertices to be aligned with the grid
newsim.set_magnetic_grid(dx=dx, dy=dy, origx=origx, origy=origy)

# set the external border of the mesh to be the contour defined above
newsim.set_external_border_vector(contour)

# set the size of the mesh to be dx and dy (in meters)
newsim.set_mesh_fine_size(dx=dx, dy=dy)

# add the block defined by the contour to the mesh
newsim.add_block(contour, dx=dx, dy=dy)

# create the mesh
if newsim.mesh():
    print('Meshing done!')
else:
    print('Meshing failed!')

# create the fine arrays with prescribed friction coefficient and turbulence
friction_coefficient = 1e-4
newsim.create_fine_arrays(default_frot=friction_coefficient, with_tubulence=True)
newsim.parameters.blocks[0].set_lateral_friction_coefficient(lateral_friction_coefficient=friction_coefficient) # add friction coefficient to the lateral walls
newsim.create_sux_suy() # find the borders where BC can be applied

Meshing done!

Get general information on the mesh

print(newsim.get_header())

Shape  : 1006 x 66
Resolution  : 0.01 x 0.01
Spatial extent :
   - Origin : (-0.03 ; -0.03)
   - End : (10.030000000000001 ; 0.63)
   - Width x Height : 10.06 x 0.66
   - Translation : (0.0 ; 0.0)
Null value : 0.0

The origin is not (0.,0.) because the meshing process adds 3 cells around all sides of the domain. This is done to ensure that there is enough space to store neighborhood relationships between blocks in the matrices and to keep at least one fringe hidden all around.

The same information is available with the function get_header_MB, which also returns the number of blocks. In this case, block1 has the correct origin at (0, 0).

print(newsim.get_header_MB())

Shape  : 1006 x 66
Resolution  : 0.01 x 0.01
Spatial extent :
   - Origin : (-0.03 ; -0.03)
   - End : (10.030000000000001 ; 0.63)
   - Width x Height : 10.06 x 0.66
   - Translation : (0.0 ; 0.0)
Null value : 0.0

Number of blocks : 1

Block block1 :

Shape  : 1006 x 66
Resolution  : 0.01 x 0.01
Spatial extent :
   - Origin : (0.0 ; 0.0)
   - End : (10.06 ; 0.66)
   - Width x Height : 10.06 x 0.66
   - Translation : (-0.03 ; -0.03)
Null value : 0.0

Visualize the topopography

fig, ax = newsim.top.plot_matplotlib()
contour.plot_matplotlib(ax)

fig.set_size_inches(15, 3)

Set the simulation parameters

nb_timesteps sets how many timesteps are performed. The writing_frequency and writing_mode keys specify how often the simulation results are saved. Avoid saving results with a large frequency to reduce the file dimension.

Avoid too large CourantNumber (must be \(\leq 1\), preferably \(\leq 0.6\)). However, too small values reduce the timestep, hence increase the computation time.

When visualizing the results, if a checkerboard pattern is observed in the water heights, it very often means that the Courant number is too high. You should then reduce it to avoid this problem.

# time parameters
newsim.parameters.set_params_time_iterations(nb_timesteps=100, optimize_timestep=True,
                                             writing_frequency=0.5, writing_mode='Seconds',
                                             initial_cond_reading_mode='Binary',
                                             writing_type='Binary compressed')

# numerical parameters
newsim.parameters.set_params_temporal_scheme(RungeKutta='RK21', CourantNumber=0.35)

# turbulence parameters
newsim.parameters.blocks[0].set_params_turbulence('k-eps HECE', maximum_nut=1e-2) # if needed, increase maximum_nut to avoid numerical issues
newsim.parameters.blocks[0].set_params_surface_friction(model_type='Horizontal and Lateral external borders (Colebrook)') # choose the right function

Print the temporal parameters of the simulation.

newsim.parameters.get_params_temporal_scheme()

{'RungeKutta': 0.3, 'CourantNumber': 0.35, 'dt_factor': 100.0}

Print the iteration parameters.

newsim.parameters.get_params_time_iterations()

{'nb_timesteps': 100,
 'optimize_timestep': 1,
 'first_timestep_duration': 0.1,
 'writing_frequency': 0.5,
 'writing_mode': 'Seconds',
 'writing_type': 'Binary compressed',
 'initial_cond_reading_mode': 'Binary',
 'writing_force_onlyonestep': 0}

Verify the simulation parameters

Several levels of verbosity are available:

• 0: Errors only

• 1: Errors and Warnings

• 2: Errors, Warnings, and Information

• 3: Errors, Warnings, Information, and section headers

print(newsim.check_all(verbosity=3))

Checking Global Parameters
--------------------------

Time/Iterations
****************

Temporal scheme
****************
Runge-Kutta is valid : 0.3
Courant number is valid : 0.35
dt factor is valid : 100.0

Collapsible building (only global values -- activation depends on the block's param)
********************
Hmax is valid : 0.0
Vmax is valid : 0.0
Qmax is valid : 0.0


Checking Block 1
----------------

Topography operator
*******************
Info : Mean operator

Reconstruction type
********************
Info : Internal reconstruction is constant
Info : Frontier reconstruction is linear with limitation
Info : Free border reconstruction is constant
Info : Number of neighbors for limitation is correct
Info : Limitation of h or h+z is correct
Info : Treatment of frontiers is correct

Flux type
**********
Info : HECE original

Froude max
**********
Info : Froude max is 20.0
Warning : Froude max is high -- Is it useful ?

Conflict resolution
********************
Info : Original conflict resolution

Sediment model
**************
Info : Sediment model not activated
Info : No drifting

Gravity discharge
*****************
Info : Gravity discharge not activated

Steady sediment
****************
Info : Not yet implemented -- Feel free to complete the code -- check_params_steady_sediment

Unsteady topo_bathymetry
***********************
Info : Unsteady topo not activated

Collapse building
*****************
Info : Collapse building not activated

Mobile Contour
**************
Info : Mobile contour not activated

Mobile Forcing
**************
Info : Mobile forcing not activated

Forcing
*******
Info: No forcing

Bridges
*******
Info : Bridges not activated
Info : Bridges file not found

Danger map
*********
Info : Danger map not activated

Turbulence
**********
Info: HECE k-eps model selected
Warning : a too low value of "max_nut" can influence the results -- To be checked by the user in the results

Infiltration
************
Info: No infiltration

Get boundary cells and set boundary conditions

Listing

The list of boundary condition edges can be obtained via list_pot_bc_x and list_pot_bc_y.

The return of these routines consists of a list of 2 Numpy vectors (np.int32). It is therefore quite easy to perform sorting or other actions to select specific edges.

• bcx[0] = indices i

• bcx[1] = indices j

These edges are numbered according to the Fortran convention, i.e., 1-based.

bcx = newsim.list_pot_bc_x()
bcy = newsim.list_pot_bc_y()

print(f'Potential boundary cells in x direction: {bcx}\n')
print(f'Potential boundary cells in y direction: {bcy}')

Potential boundary cells in x direction: (array([   4,    4,    4,    4,    4,    4,    4,    4,    4,    4,    4,
          4,    4,    4,    4,    4,    4,    4,    4,    4,    4,    4,
          4,    4,    4,    4,    4,    4,    4,    4,    4,    4,    4,
          4,    4,    4,    4,    4,    4,    4,    4,    4,    4,    4,
          4,    4,    4,    4,    4,    4,    4,    4,    4,    4,    4,
          4,    4,    4,    4,    4,  104,  104,  104,  104,  104,  104,
        104,  104,  104,  104,  104,  104,  119,  119,  119,  119,  119,
        119,  119,  119,  119,  119,  119,  119,  204,  204,  204,  204,
        204,  204,  204,  204,  204,  204,  204,  204,  219,  219,  219,
        219,  219,  219,  219,  219,  219,  219,  219,  219,  304,  304,
        304,  304,  304,  304,  304,  304,  304,  304,  304,  304,  319,
        319,  319,  319,  319,  319,  319,  319,  319,  319,  319,  319,
        404,  404,  404,  404,  404,  404,  404,  404,  404,  404,  404,
        404,  419,  419,  419,  419,  419,  419,  419,  419,  419,  419,
        419,  419,  504,  504,  504,  504,  504,  504,  504,  504,  504,
        504,  504,  504,  519,  519,  519,  519,  519,  519,  519,  519,
        519,  519,  519,  519,  604,  604,  604,  604,  604,  604,  604,
        604,  604,  604,  604,  604,  619,  619,  619,  619,  619,  619,
        619,  619,  619,  619,  619,  619, 1004, 1004, 1004, 1004, 1004,
       1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004,
       1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004,
       1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004,
       1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004,
       1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004, 1004],
      dtype=int32), array([ 4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
       21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37,
       38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54,
       55, 56, 57, 58, 59, 60, 61, 62, 63, 52, 53, 54, 55, 56, 57, 58, 59,
       60, 61, 62, 63, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,  4,
        5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15,  4,  5,  6,  7,  8,  9,
       10, 11, 12, 13, 14, 15, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62,
       63, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,  4,  5,  6,  7,
        8,  9, 10, 11, 12, 13, 14, 15,  4,  5,  6,  7,  8,  9, 10, 11, 12,
       13, 14, 15, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 52, 53,
       54, 55, 56, 57, 58, 59, 60, 61, 62, 63,  4,  5,  6,  7,  8,  9, 10,
       11, 12, 13, 14, 15,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15,
        4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
       21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37,
       38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54,
       55, 56, 57, 58, 59, 60, 61, 62, 63], dtype=int32))

Potential boundary cells in y direction: (array([   4,    4,    5, ..., 1002, 1003, 1003], dtype=int32), array([ 4, 64,  4, ..., 64,  4, 64], dtype=int32))

# X borders - 0-based
lmost = int(np.asarray(bcx[0]).min())
rmost = int(np.asarray(bcx[0]).max())

# Y borders - 0-based
ymin = int(np.asarray(bcx[1]).min())
ymax = int(np.asarray(bcx[1]).max())

print(f'Bottom-left cell coordinates: {(lmost, ymin)}')
print(f'Top-right cell coordinates: {(rmost, ymax)}')

Bottom-left cell coordinates: (4, 4)
Top-right cell coordinates: (1004, 63)

Visualize boundary cells (blue for horizontal and red for vertical boundaries).

%matplotlib inline

fig, ax = newsim.plot_borders(xy_or_ij='xy', xcolor='b', ycolor='r')
ax.set_xticks(np.arange(newsim.origx, newsim.endx, newsim.dx))
ax.set_yticks(np.arange(newsim.origy, newsim.endy, newsim.dy))
ax.grid()
fig.set_size_inches(15, 5)

Imposing a Weak Condition

It is possible to impose a weak condition via the add_weak_bc_x and add_weak_bc_y routines.

The following arguments must be specified:

• the indices (i, j) as available in the previous lists

• the type of BC BCType_2D (longitudinal and lateral unit discharge, QX and QY; water level, H)

• the value (this value does not matter for NONE, except for 99999., which is equivalent to a null value in previous versions)

newsim.reset_all_boundary_conditions()

# unit discharge at the leftmost X cells (upstream BC)
for j in range(ymin, ymax+1):
    newsim.add_weak_bc_x(i = lmost, j = j, ntype = BCType_2D.QX, value = Qx_ups)
    newsim.add_weak_bc_x(i = lmost, j = j, ntype = BCType_2D.QY, value = 0.0) # no lateral flow

# water depth at the rightmost X cells (downstream BC)
for j in range(ymin, ymax+1):
    newsim.add_weak_bc_x(i = rmost, j = j, ntype = BCType_2D.H, value = h_dws)

Set initial conditions and other simulation parameters

Initial channel topography

top = newsim.read_fine_array('.top') # get a WolfArray object

# create channel elevation row - no need to create a complete 2D array
x = np.arange(0, Lx, dx)
z = - slope * x

# copy the channel bed elevation to each row of the top.array
for j in range(ymin, ymax+1):
    top.array[lmost:rmost, j] = z

# # if the bed elevation is constant, you can also set the whole array to the same value
# top.array[:,:] = 0.0

print('Topo min : ', top.array.min())
print('Topo max : ', top.array.max())

top.write_all()

Topo min :  -0.0
Topo max :  -0.0

Initial water depth

h = newsim.read_fine_array('.hbin')

# since topography is flat, the water height matrix can be easily edited
h.array[:,:] = h_dws

print('Hauteur min : ', h.array.min())
print('Hauteur max : ', h.array.max())

h.write_all()

Hauteur min :  0.058
Hauteur max :  0.058

Flow rates through X and Y

qx = newsim.read_fine_array('.qxbin')
qy = newsim.read_fine_array('.qybin')

qx.array[:,:] = 0.
qy.array[:,:] = 0.

qx.write_all()
qy.write_all()

Friction coefficient

Default law is Manning-Strickler.

nManning = newsim.read_fine_array('.frot')

print('Default friction value: ', nManning.array.max())

Default friction value:  1e-04

Final checks and saving simulation

Saving to Disk

Parameters and boundary conditions can be saved to disk in the “.par” file using the save method.

Writing to disk can only be properly performed after defining both the useful parameters and the boundary conditions of the problem.

newsim.save()

WARNING:root:No infiltration data to write

You can verify the date of the last modification of the new simulation topography (or any other array).

print('Last modified (UTC) : ', newsim.last_modification_date('.top', tz.utc)) # date in UTC

Last modified (UTC) :  2025-05-30 13:06:03.100049+00:00

It is possible to easily read data using read_fine_array or read_MB_array by passing the file extension as an argument.

The ‘.’ in the extension is optional but recommended for better readability.

The return is a WolfArray or WolfArrayMB object (see WolfArray Documentation).

# example of reading the napbin matrix
nap  = newsim.read_fine_array('.napbin')
nap2 = newsim.read_fine_array('napbin')

print('Comparison of matrix characteristics: ', nap2.is_like(nap))
print('Value comparison: ', np.all(nap2.array.data == nap.array.data))
print('Mask comparison: ', np.all(nap2.array.mask == nap.array.mask))

Comparison of matrix characteristics:  True
Value comparison:  True
Mask comparison:  True

Run the simulation

Once all the files are written to disk, it’s time to start the calculation.

To do so, either run the next cell newsim.run_wolfcli or execute the command wolfcli run_wolf2d_prev genfile=pathtosim in a command window, provided that wolfcli is accessible (e.g., via the PATH).

How to do so:

1. Open the Windows menu (Windows logo or Ctrl+Esc)

2. Type cmd

3. Open Command Prompt

4. Type cd pathtosim

5. Type wolfcli run_wolf2d_prev genfile=pathtosim

Make sure to replace pathtosim with the actual directory where this notebook is stored

(something similar to C:\Users\yourname\Desktop\gitlabrepository\simulations).

Attention: do not run the cells following the next one before the calculation has finished! Otherwise, the python kernel will crash as the simulation files are being overwritten.

newsim.run_wolfcli()

Access the results

If the calculation proceeded as expected, additional files will be present in your simulation directory.

These include:

• .RH : results of water height on the calculated meshes (binary - float32)

• .RUH : results of specific discharge along X (binary - float32)

• .RVH : results of specific discharge along Y (binary - float32)

• .RCSR : mesh numbering according to the Compressed Sparse Row standard (binary - int32)

• .HEAD : header containing all position information in the previous files (binary - mixed)

• .RZB : result of bottom elevation (sediment calculation)

Additional files will be present in case of turbulence calculation, depending on the chosen model.

It is recommended to access the results via the Wolfresults_2D class - Wolfresults_2D API.

# generate instance of the result object
res = Wolfresults_2D(newsim.filename)

# get number of results
n_res = res.get_nbresults()

print('Number of results: ', res.get_nbresults())

Number of results:  107

You can extract the stored times and the timesteps.

# extract time and timesteps
times, timesteps = res.get_times_steps()
print('Times: ', times)
print('Timesteps: ', timesteps)

Times:  [ 0.         0.5015121  1.0023386  1.5016546  2.001919   2.5024412
  3.0013795  3.5011578  4.0014176  4.502446   5.000809   5.502084
  6.001237   6.5023127  7.0011334  7.5017495  8.0009365  8.500862
  9.001777   9.501919  10.002204  10.502583  11.001969  11.501813
 12.001568  12.502362  13.001185  13.500698  14.000468  14.5026045
 15.002597  15.502099  16.001596  16.501358  17.000643  17.50115
 18.002254  18.501984  19.000114  19.5023    20.001415  20.5012
 21.000227  21.500643  22.001781  22.502323  23.001415  23.501835
 24.001543  24.501318  25.001766  25.5022    26.000576  26.502256
 27.002222  27.500095  28.002329  28.500319  29.001446  29.501617
 30.002073  30.5004    31.001257  31.500914  32.001945  32.50202
 33.001144  33.501354  34.000206  34.50019   35.00138   35.50133
 36.002228  36.50133   37.00134   37.502007  38.000797  38.50038
 39.00075   39.502388  40.00085   40.501328  41.00063   41.50236
 42.002472  42.50074   43.000004  43.50125   44.00041   44.50245
 45.000984  45.502403  46.000904  46.501858  47.00083   47.501087
 48.00019   48.50211   49.001907  49.502216  50.000755  50.500492
 51.000793  51.50174   52.00254   52.50011   53.002586 ]
Timesteps:  [    0   157   315   491   671   848  1027  1205  1384  1564  1742  1922
  2099  2278  2456  2635  2813  2991  3169  3348  3528  3709  3889  4069
  4250  4432  4614  4796  4978  5162  5346  5530  5715  5900  6085  6271
  6458  6647  6839  7035  7232  7431  7631  7833  8036  8239  8441  8643
  8845  9048  9253  9459  9664  9870 10075 10279 10485 10690 10897 11104
 11311 11516 11721 11925 12129 12332 12534 12736 12937 13138 13339 13539
 13739 13938 14137 14336 14534 14732 14930 15128 15324 15520 15715 15911
 16106 16300 16495 16691 16886 17082 17276 17470 17662 17855 18047 18239
 18430 18622 18813 19004 19194 19384 19574 19764 19954 20143 20334]

# get result from one specific timestep (0-based)
res.read_oneresult(-1)

The results are stored in the form of blocks, accessible via a dictionary. The key for this dictionary is generated by the getkeyblock function from the wolf_array module, WolfArray API.

Each block contains the results for various unknowns and, if applicable, combined values.

It is possible to choose these combined values via the views_2D Enum - Views_2D API.

The current view of a result object allows to visualize and analyze the defined variable.

res.set_current(views_2D.WATERDEPTH) # set the current view to water depth

The matrix of each block can be obtained in three different ways as done in the next cell.

fr1 = res[0]                              # result matrix of block #1 by passing an integer
fr2 = res[getkeyblock(1, addone=False)]   # result matrix of block #1 by passing a key generated by getkeyblock
fr3 = res[getkeyblock(0)]                 # result matrix of block #0 by passing a key generated by getkeyblock

assert fr1 == fr2
assert fr2 == fr3

print('Result type: ', type(fr1))   # returned format is of type "WolfArray"

Result type:  <class 'wolfhece.wolf_array.WolfArray'>

Visualize the results

It is possible to visualize the results of a specific timestep by defining this.

ts_result = -1

# get the result of the specified timestep
res.read_oneresult(ts_result)

# set current view to the desired variable
res.set_current(views_2D.WATERDEPTH)
print('Minimum water depth: ', res[0].array.min())
print('Maximum water depth: ', res[0].array.max())

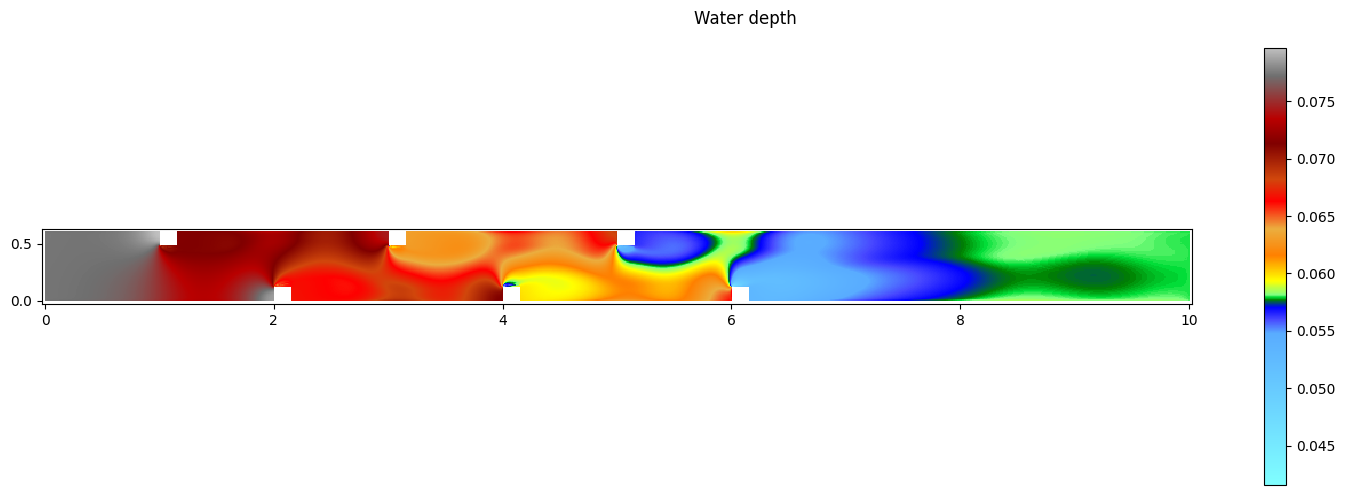
fig,ax = res[0].plot_matplotlib()
fig.suptitle('Water depth')
fig.colorbar(ax.images[0], ax=ax)
fig.set_size_inches(15, 5)
fig.tight_layout()

Minimum water depth:  0.041603282
Maximum water depth:  0.07961363

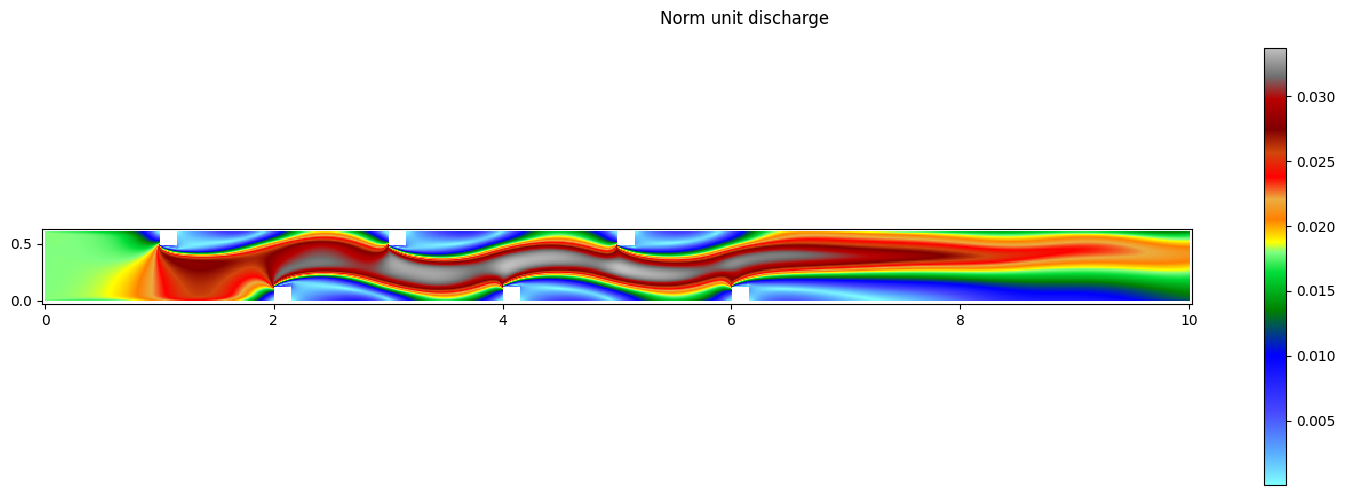
res.set_current(views_2D.QNORM)
print('Minimum norm unit discharge:', res[0].array.min())
print('Maximum norm unit discharge:', res[0].array.max())

fig,ax = res[0].plot_matplotlib()
fig.suptitle('Norm unit discharge')
fig.colorbar(ax.images[0], ax=ax)
fig.set_size_inches(15, 5)
fig.tight_layout()

Minimum norm unit discharge: 5.2852378e-05
Maximum norm unit discharge: 0.03371695

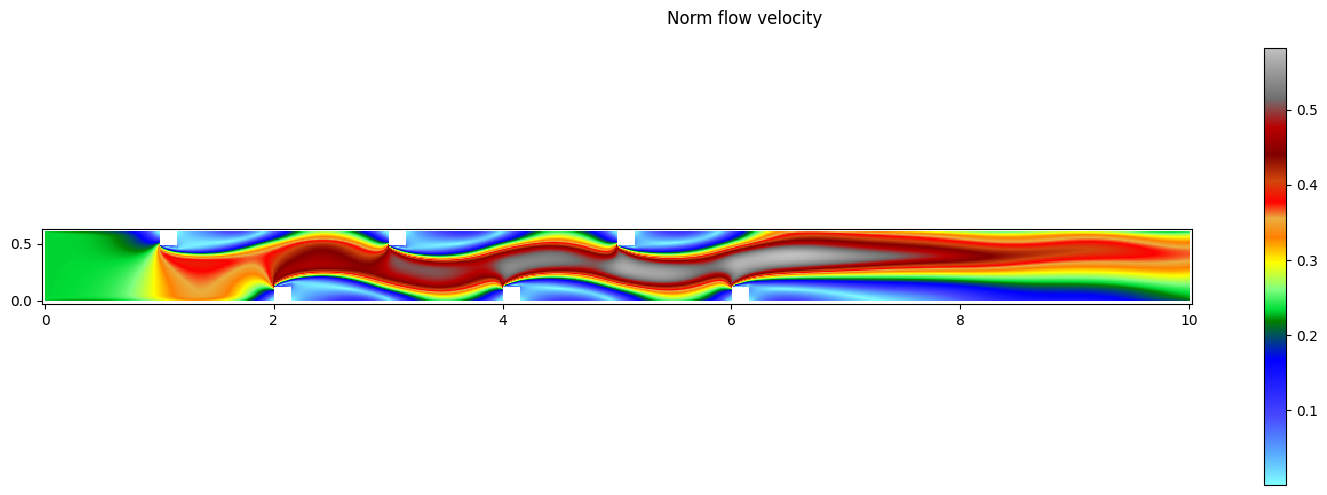
res.set_current(views_2D.UNORM)
print('Minimum norm flow velocity:', res[0].array.min())
print('Maximum norm flow velocity:', res[0].array.max())

fig,ax = res[0].plot_matplotlib()
fig.suptitle('Norm flow velocity')
fig.colorbar(ax.images[0], ax=ax)
fig.set_size_inches(15, 5)
fig.tight_layout()

Minimum norm flow velocity: 0.00089196354
Maximum norm flow velocity: 0.58194137

Generate an animation of the results

Create arrays for the x- and y-axis and ticks for the animation.

nbx, nby=int(Lx/dx), int(Ly/dy)

# generate x- and y-axis arrays
x_axis = np.arange(origx, nbx+1, 50)
y_axis = np.arange(origy, nby+1, 30)

# generate x- and y-axis ticks
x_ticks = np.arange(origx, Lx+dx, 0.5)
y_ticks = np.arange(origy, Ly+dy, 0.3)

Get the minimum and maximum velocities to set a constant colorbar for the animation.

# get min/max velocities from last time step
res.read_oneresult(-1)
res.set_current(views_2D.UNORM)
u = res[0].array.T
u_min, u_max = u.min(), u.max()

vmin = 0 if u_min >= 0 else u_min
vmax = 0 if u_max < 0 else u_max

Generate the first frame of the animation (first timestep).

%matplotlib inline

# generate animation
init=0 # initial animation timestep
interv=1 # interval between frames
spacing = range(init, n_res, interv) # timesteps to be animated

fig, ax = plt.subplots(figsize=(15, 5))

# first frame setup
res.read_oneresult(spacing[init])
res.set_current(views_2D.UNORM)
im = ax.imshow(res[0].array.T, cmap='jet', interpolation='nearest', vmin=vmin, vmax=vmax)
ax.set_title(f'{simulation_name} simulation norm velocity - time {times[0]} s', fontsize=16)
ax.set_xlabel('X [m]', fontsize=14)
ax.set_ylabel('Y [m]', fontsize=14)
ax.set_xticks(ticks=x_axis, labels=x_ticks, fontsize=14)
ax.set_yticks(ticks=y_axis, labels=y_ticks, fontsize=14)
ax.invert_yaxis()

cbar = fig.colorbar(im, ax=ax, orientation='horizontal', fraction=0.05, pad=0.13)
fig.tight_layout()

Define a function to update the frames of the animation.

Make sure that views_2D. is set to the same variable as the previous cell!

def update(time, timestep):
    res.read_oneresult(timestep)
    res.set_current(views_2D.UNORM)
    ax.clear()
    im = ax.imshow(res[0].array.T, cmap='jet', interpolation='nearest', vmin=0, vmax=0.45)
    title = ax.set_title(f'{simulation_name} simulation norm velocity - time {time} s', fontsize=16)
    ax.set_xlabel('X [m]', fontsize=14)
    ax.set_ylabel('Y [m]', fontsize=14)
    ax.set_xticks(ticks=x_axis, labels=x_ticks, fontsize=14)
    ax.set_yticks(ticks=y_axis, labels=y_ticks, fontsize=14)
    ax.invert_yaxis() # because WolfArrays are flipped
    fig.tight_layout()
    return im, title

Generate the animation using the function defined above.

%matplotlib inline
ani = animation.FuncAnimation(
    fig,
    func=lambda i: update(times[i], spacing[i]),
    frames=len(spacing),
    interval=500,  # milliseconds per frame
    blit=False  # True is not supported with custom plot function
)

d:\ProgrammationGitLab\python3.11\Lib\site-packages\matplotlib\animation.py:908: UserWarning: Animation was deleted without rendering anything. This is most likely not intended. To prevent deletion, assign the Animation to a variable, e.g. `anim`, that exists until you output the Animation using `plt.show()` or `anim.save()`.
  warnings.warn(

Save the animation if needed.

Make sure that the variable UNORM is updated if another variable is animated.

save_ani = False # set to True to save the animation
if save_ani:
    ani.save(f"plots\WOLF_simulations\{simulation_name}_UNORM.mp4",
             writer='ffmpeg', dpi=150)

Display the animation in the notbeook.

%matplotlib inline
HTML(ani.to_jshtml())

Once Loop Reflect