Analyse de hauteurs d’eau pour les bâtiments du PICC
Import des modules
[ ]:
# import _add_path # for debugging purposes only - can be removed in production
try:
from wolfhece import is_enough
if not is_enough('2.2.32'):
raise ImportError("Please update wolfhece to at least version 2.2.31")
except ImportError:
raise ImportError("Please install the required version of wolfhece: pip install wolfhece>=2.2.30")
from wolfhece.analyze_poly import Building_Waterdepth_analysis
from wolfhece.wolf_array import WolfArray, header_wolf
from wolfhece.PyVertexvectors import vector, zone, Zones, wolfvertex as wv
from wolfhece.pydownloader import toys_dataset
from wolfhece.PyPalette import wolfpalette as wp
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pathlib import Path
Lecture de matrices
[2]:
T = [2, 5, 15, 25, 50, 100, 1000]
dir_arrays = 'Analysis_PICC_poly'
arrays = {f"T{t}": WolfArray(toys_dataset(dir_arrays, f"T{t}.tif")) for t in T}
[3]:
print(arrays['T2'])
Shape : 1964 x 4218
Resolution : 1.0 x 1.0
Spatial extent :
- Origin : (251619.0 ; 135545.0)
- End : (253583.0 ; 139763.0)
- Width x Height : 1964.0 x 4218.0
- Translation : (0.0 ; 0.0)
Null value : 0.0
Création de l’objet d’analyse
[4]:
# On passe les matrices sous la forme d'un dictionnaire dont les clés seront exploités pour les légendes
analyze = Building_Waterdepth_analysis(arrays= arrays,
zones= toys_dataset('PICC', 'PICC_Vesdre.shp'),
merge_zones=True, # merge all buildings into one zone - otherwise, each building will be a separate zone
)
[5]:
analyze.all_categories
[5]:
['Administration',
'Agricole',
'Annexe',
'Commerce ou service',
'Culture, sport ou loisir',
'Gare',
'Habitation',
'Industriel',
'Lieu de culte',
'Maison de repos',
'Police',
'Pompier',
'Scolaire',
'Scolaire fondamental',
'Scolaire secondaire',
'Station service']
Comptage du nombre de polygones avec valeurs
[6]:
df = analyze.count_strictly_positive_as_df()
print(df)
Zone Array Count
0 all T2 64
1 all T5 168
2 all T15 384
3 all T25 693
4 all T50 993
5 all T100 1331
6 all T1000 1999
Graphique du nombre de polygones contenant des valeurs strictement positives
[7]:
analyze.plot_count_strictly_positive()
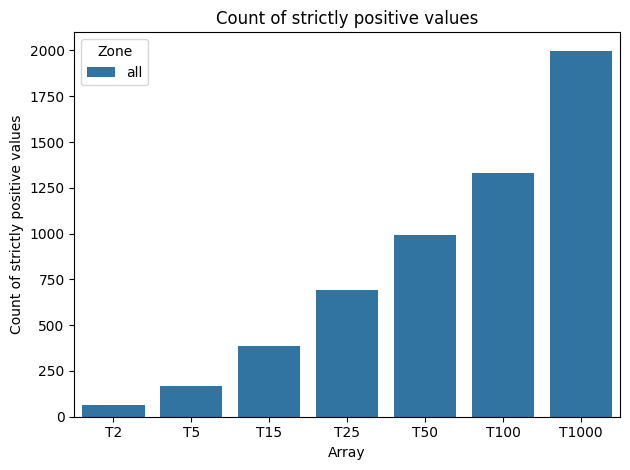
[7]:
(<Figure size 640x480 with 1 Axes>,
<Axes: title={'center': 'Count of strictly positive values'}, xlabel='Array', ylabel='Count of strictly positive values'>)
Graphique de la distribution des valeurs
[8]:
analyze.plot_distributed_values(bins = [0., .3, 1.3, 2.5, 4, -1],
operator= 'Mean',
merge_zones= True,
engine= 'seaborn')
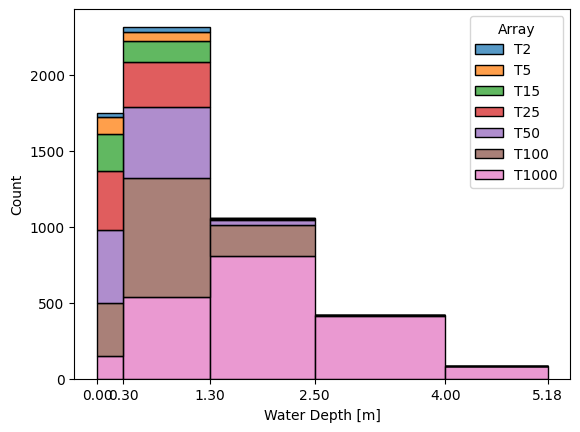
[8]:
(<Figure size 640x480 with 1 Axes>,
<Axes: xlabel='Water Depth [m]', ylabel='Count'>)
Sélection de certains types de bâtiments
On a vu un peu plus tôt comment afficher les catégories disponibles:
‘Agricole’,
‘Culture, sport ou loisir’,
‘Station service’,
‘Habitation’,
‘Annexe’,
‘Pompier’,
‘Gare’,
‘Police’,
‘Scolaire fondamental’,
‘Industriel’,
‘Maison de repos’,
‘Administration’,
‘Scolaire secondaire’,
‘Commerce ou service’,
‘Scolaire’,
‘Lieu de culte’
[9]:
analyze.active_categories = ['Habitation']
analyze.plot_count_strictly_positive()
analyze.plot_distributed_values(bins = [0., .3, 1.3, 2.5, 4, -1],
operator= 'Mean',
merge_zones= True,
engine= 'seaborn')
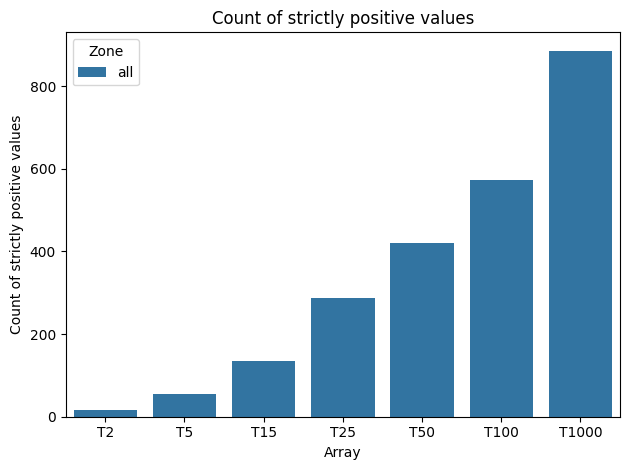
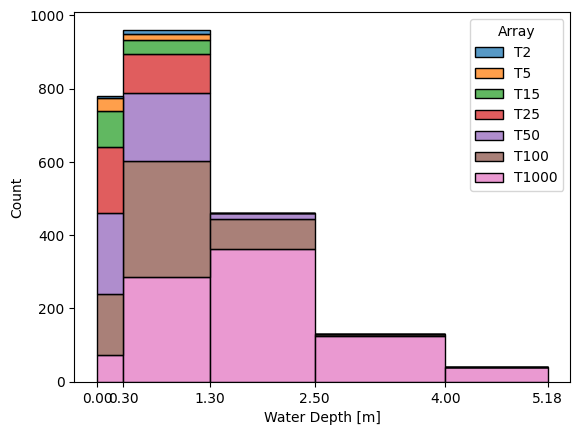
[9]:
(<Figure size 640x480 with 1 Axes>,
<Axes: xlabel='Water Depth [m]', ylabel='Count'>)
Graphique des surfaces concernées
Il est également possible de n’activer que certaines matrices.
[10]:
analyze.active_arrays = analyze.all_arrays
analyze.deactivate_array('T1000')
analyze.deactivate_array('T100')
analyze.plot_distributed_areas(bins = [0., .3, 1.3, 2.5, 4, -1],
operator= 'Mean',
merge_zones= True)
print('Matrices actives : ', analyze.active_arrays)
print('Catégories actives : ', analyze.active_categories)
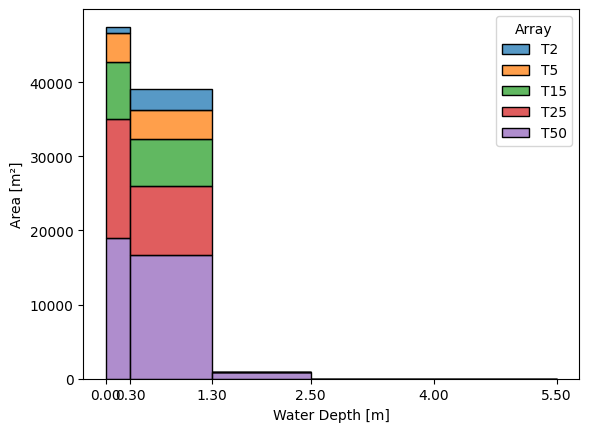
Matrices actives : ['T2', 'T5', 'T15', 'T25', 'T50']
Catégories actives : ['Habitation']
Récupération d’une zone pour l’affichage
L’objet analyze permet de récupérer les zones des polygones analysés, sur base des catégories et des matrices activées.
Une ‘zone’ sera créée pour chaque matrice activée.
[11]:
zone2plot = analyze.as_zones()
print(zone2plot.mynames)
['T2', 'T5', 'T15', 'T25', 'T50']
Paramétrage de la zone :
set_filled(True)pour remplir les polygones,set_colors_from_value('Mean', cmap=cmap, vmin=0, vmax=4)pour colorer les polygones en fonction de la valeur moyenne des hauteurs d’eau, avec une palette de couleurs définie parcmap.
[12]:
zone2plot.set_filled(True)
cmap = wp()
cmap.default16()
cmap.distribute_values(0., 5.)
zone2plot.set_colors_from_value('Mean', cmap=cmap, vmin=0, vmax=4)
Dessin des polygones
Etapes :
création d’autant de sous-graphes que de matrices activées.
pour chaque matrice activée, on affiche la matrice et un fond de plan IGN.
on affiche les polygones de la zone créée précédemment.
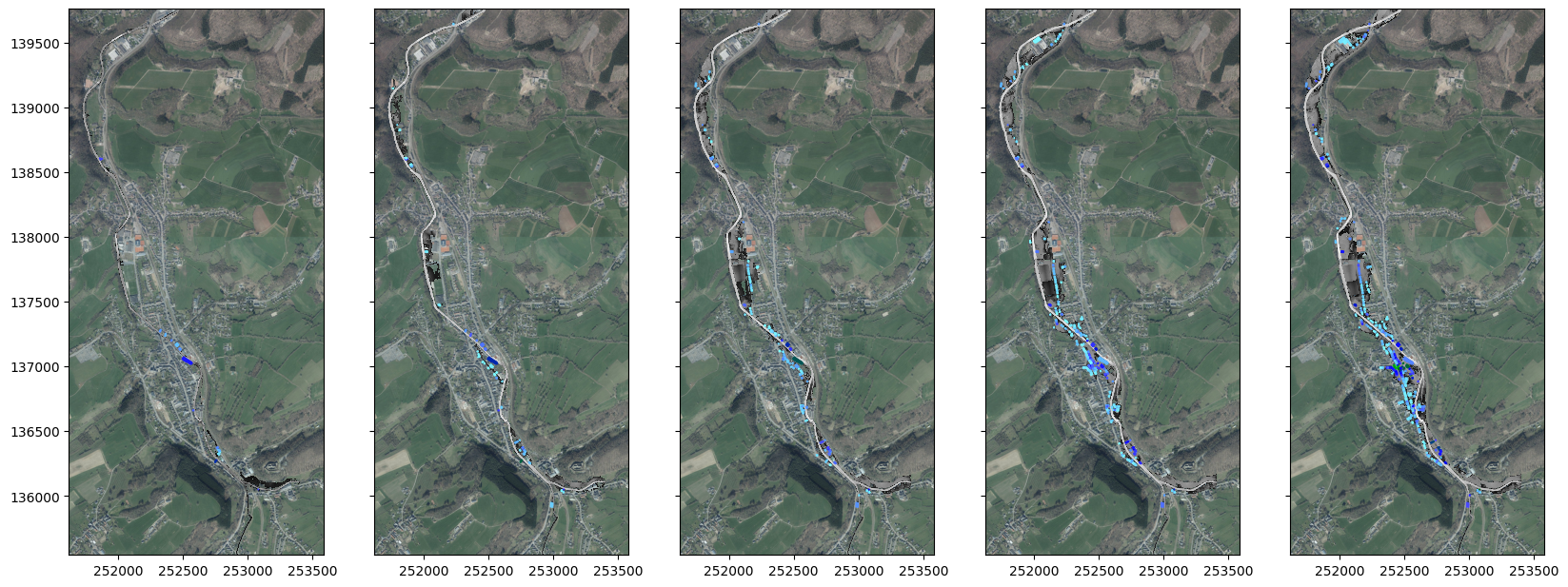
[13]:
# %matplotlib widget
fig, ax = plt.subplots(1,5, figsize=(20, 20), sharey='row', sharex='row')
for i, key in enumerate(zone2plot.mynames):
arrays[key].mypal.defaultgray()
arrays[key].plot_matplotlib((fig, ax[i]), IGN = True, cat = 'orthoimage_coverage_2021')
zone2plot[key].plot_matplotlib(ax[i])
ax[i].set_aspect('equal')
Récupération des valeurs sous forme de DataFrame
[14]:
df50 = analyze['T50'].get_values()
print('Nombre de polygones : ', len(df50))
Nombre de polygones : 1576
On peut ensuite trouver toutes les autres grandeurs statistiques sur les valeurs des polygones, comme la somme, la moyenne, le minimum, le maximum, etc.
[15]:
maxima = df50.max()
minima = df50.min()
p90 = df50.quantile(0.9)
print(p90)
Habitation___3 0.450813
Habitation___4 1.570447
Habitation___5 0.248419
Habitation___14 1.144392
Habitation___15 0.236443
...
Habitation___2768 0.607735
Habitation___2774 0.327185
Habitation___2791 0.615591
Habitation___2793 0.136333
Habitation___2806 0.399887
Name: 0.9, Length: 421, dtype: float64
Récupération des géométries sous forme de DataFrame
Le dataframe contient :
les coordonnées des centroids des polygones sous forme de Point (Shapely) et sous forme de coordonnées X et Y,
la géométrie des polygones sous forme de Polygons (Shapely).
[16]:
analyze['T2'].get_geometries()
[16]:
| Centroid | X | Y | Geometry | |
|---|---|---|---|---|
| Habitation___365 | POINT (252578.20644290387 136661.75737353018) | 252578.206443 | 136661.757374 | POLYGON ((252582.94600000232 136659.3898000009... |
| Habitation___410 | POINT (251865.23978716985 138603.36743561501) | 251865.239787 | 138603.367436 | POLYGON ((251862.51299999654 138603.2758000008... |
| Habitation___758 | POINT (252772.58743948632 136357.6868196059) | 252772.587439 | 136357.686820 | POLYGON ((252773.40299999714 136357.2417999990... |
| Habitation___767 | POINT (252784.93215005085 136341.31213371415) | 252784.932150 | 136341.312134 | POLYGON ((252790.3650000021 136340.31679999828... |
| Habitation___883 | POINT (252323.63143596248 137277.06658775956) | 252323.631436 | 137277.066588 | POLYGON ((252331.30099999905 137284.5667999982... |
| Habitation___885 | POINT (252773.2139256541 136328.34762762696) | 252773.213926 | 136328.347628 | POLYGON ((252780.64299999923 136329.3528000004... |
| Habitation___1199 | POINT (252410.0295237607 137201.88507863414) | 252410.029524 | 137201.885079 | POLYGON ((252416.6799999997 137202.84980000183... |
| Habitation___1259 | POINT (252780.1457208407 136349.35527273448) | 252780.145721 | 136349.355273 | POLYGON ((252787.9680000022 136346.9987999983,... |
| Habitation___1695 | POINT (253080.48830737371 136050.9957918227) | 253080.488307 | 136050.995792 | POLYGON ((253078.31769999862 136048.2879000008... |
| Habitation___1783 | POINT (252362.85480023528 137243.4041296981) | 252362.854800 | 137243.404130 | POLYGON ((252369.33299999684 137254.7947999984... |
| Habitation___1873 | POINT (252752.37265091634 136269.89060153702) | 252752.372651 | 136269.890602 | POLYGON ((252761.24899999797 136275.6917999982... |
| Habitation___2292 | POINT (252764.6561770505 136373.69342816217) | 252764.656177 | 136373.693428 | POLYGON ((252773.41200000048 136373.2578000016... |
| Habitation___2397 | POINT (252530.13401562328 137045.56626955583) | 252530.134016 | 137045.566270 | POLYGON ((252520.64310000092 137063.7829999998... |
| Habitation___2523 | POINT (252452.3326791363 137168.09434894653) | 252452.332679 | 137168.094349 | POLYGON ((252465.28700000048 137171.0007999986... |
| Habitation___2544 | POINT (252778.3285363715 136322.41603772016) | 252778.328536 | 136322.416038 | POLYGON ((252785.46400000155 136323.3817999996... |
| Habitation___2691 | POINT (252475.51498097405 137134.79409508978) | 252475.514981 | 137134.794095 | POLYGON ((252478.82500000298 137139.1717999987... |
Conversion en GeoDataFrame
Cela peut être utile pour traiter les données géographiques avec des bibliothèques comme GeoPandas.
[17]:
import geopandas as gpd
# convert the DataFrame to a GeoDataFrame
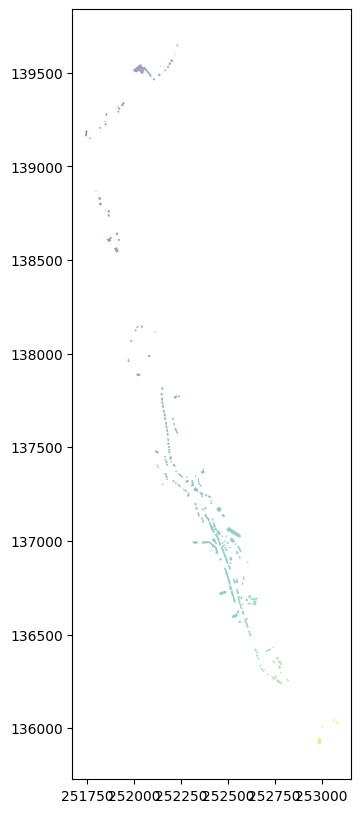
gdf50 = gpd.GeoDataFrame(analyze['T50'].get_geometries(), geometry='Geometry')
gdf50.set_crs(epsg=31370, inplace=True) # set the coordinate reference system
gdf50.plot(column='X', figsize=(10, 10), markersize=5, alpha=0.5)
[17]:
<Axes: >
Fusion des géométries avec les valeurs
On peut également fusionner les géométries avec les valeurs pour obtenir un GeoDataFrame contenant à la fois les géométries et les valeurs des polygones.
[18]:
maxima = pd.Series(df50.max(), name='Maximum') # Pour la fusion, il est préférable de créer une série avec un nom
gdf50 = gdf50.merge(maxima, left_index=True, right_index=True)
gdf50.plot(column='Maximum', figsize=(10, 10), markersize=5, alpha=0.5, cmap='viridis')
[18]:
<Axes: >
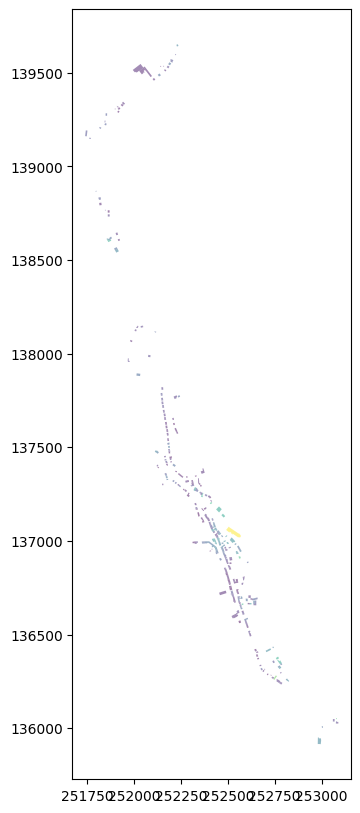
Récupération des géométries et des valeurs
Il est possible de récupérer les géométries et les valeurs des polygones sous forme de GeoDataFrame.
Dans ce cas, les valeurs sont sous la forme d’un vecteyur Numpy dans la colonne ‘Values’, et les géométries sont sous la forme de Polygons (Shapely) dans la colonne ‘Geometry’.
[19]:
gdf50 = analyze['T50'].get_geodataframe_with_values()
[20]:
gdf50.iloc[0]
[20]:
Centroid POINT (251843.7876969067 139239.45057711063)
X 251843.787697
Y 139239.450577
Geometry POLYGON ((251846.17119999975 139244.2434000000...
Values [0.3013153, 0.27349854, 0.42713928, 0.29135132...
Name: Habitation___3, dtype: object
Exemple pour trouver la valeur maximale du premier polygone :
[21]:
gdf50.iloc[0].Values.max()
[21]:
np.float32(0.55755615)
Réaliser un clustering des bâtiments touchés
On peut réaliser un clustering des polygones en utilisant la méthode clustering() de l’objet analyze. Cette méthode retourne un GeoDataFrame contenant les polygones regroupés par cluster, ainsi que les centroids et les footprints des clusters.
[22]:
gdf_cluster, (centroids, footprints) = analyze['T50'].clustering(n_clusters= 8)
Comme pour la routine ‘get_geodataframe_with_values’, les valeurs sont fournies sous la forme d’un vecteur Numpy dans la colonne ‘Values’, et les géométries sont sous la forme de Polygons (Shapely) dans la colonne ‘Geometry’.
[23]:
gdf_cluster.columns
[23]:
Index(['Centroid', 'X', 'Y', 'Geometry', 'Values', 'Cluster'], dtype='object')
Calcul, pour l’exemple, de la valeur maximale pour chaque polygone :
[24]:
# Iterate over lines and store the maximum value in a new column
for i, row in gdf_cluster.iterrows():
gdf_cluster.at[i, 'maximum'] = row['Values'].max()
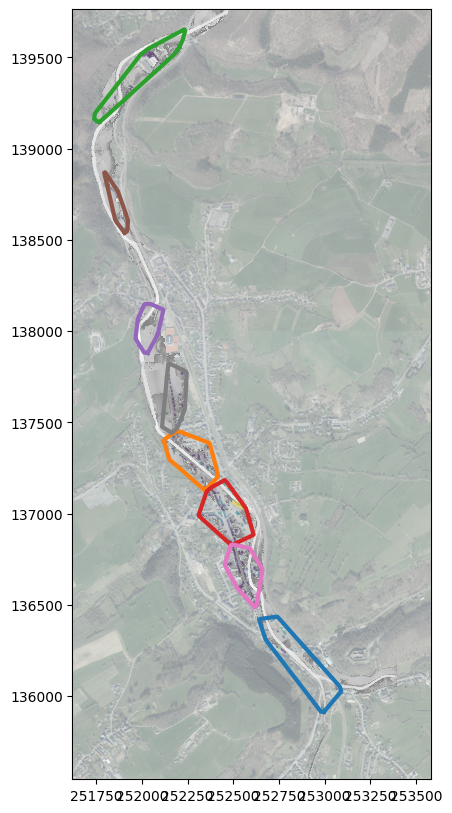
Affichage des polygones et des clusters
[25]:
fig, ax = plt.subplots(figsize=(10, 10))
ax.set_aspect('equal')
arrays['T50'].plot_matplotlib((fig, ax), IGN=True, cat='orthoimage_coverage_2021')
# Plot a white rectangle over the background to make the footprints more visible
bounds = ax.get_xlim(), ax.get_ylim()
ax.add_patch(plt.Rectangle((bounds[0][0], bounds[1][0]), bounds[0][1] - bounds[0][0], bounds[1][1] - bounds[1][0], color='white', alpha=0.5))
# Plot the clusters
for footprint in footprints:
xy = np.array(footprint.exterior.coords) # Get the coordinates of the polygon exterior
plt.plot(xy[:,0], xy[:,1], linewidth=3)
# Plot the polygons
gdf_cluster.plot(ax=ax, column='maximum', cmap='viridis', markersize=5, alpha=0.5)
[25]:
<Axes: >