Volume depuis la surface libre, combinaison (h + Z)

Il est recommandé de lire d’abord les notebooks relatifs aux calcul des ces grandeurs sur base de données d’altimétrie (seule) et de hauteur d’eau (seule).

[ ]:

# import _add_path # for debugging purposes only - must be removed in production

import numpy as np
from pathlib import Path
import matplotlib.pyplot as plt

from wolfhece import is_enough
if not is_enough('2.2.35'):
    raise ImportError("This code requires wolfhece version 2.2.34 or higher. -- try pip install wolfhece --upgrade")

from wolfhece.wolf_array import WolfArray
from wolfhece.pydownloader import toys_dataset
from wolfhece.PyVertexvectors import Zones, zone, vector, wolfvertex as wv

Importer des données de hauteurs d’eau

On importe la matrice et on masque une portion sur base d’un polygone et d’une contrainte de seuil ( h <= 0.5 m).

[13]:

el = WolfArray(toys_dataset('SurfaceVolume', 'elevation.tif'))
wd = WolfArray(toys_dataset('SurfaceVolume', 'waterdepth.tif'))

mask = Zones(toys_dataset('SurfaceVolume', 'selection.vec'))
mask_poly = mask[('selection', 'contour')]
el.mask_outsidepoly(mask_poly) # Mask the area outside the polygon
wd.mask_outsidepoly(mask_poly) # Mask the area outside the polygon

wel = el + wd  # Combine elevation and water depth to get the total water level (WEL)

print('Maximum elevation:', el.array.max(), 'm')
print('Maximum water depth:', wd.array.max(), 'm')
print('Maximum water level:', wel.array.max(), 'm')
print('Minimum water level:', wel.array.min(), 'm')

fig, ax = wel.plot_matplotlib()

ax.legend()

Maximum elevation: 184.993 m
Maximum water depth: 0.75411797 m
Maximum water level: 173.22318 m
Minimum water level: 170.69792 m

C:\Users\pierre\AppData\Local\Temp\ipykernel_416\2341108294.py:18: UserWarning: No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
  ax.legend()

[13]:

<matplotlib.legend.Legend at 0x2765c579750>

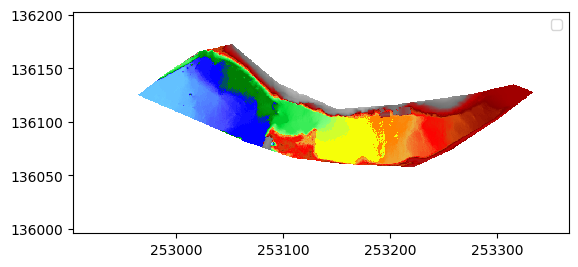
../_images/tutorials_wolfarray_surfacevolume_wel_3_3.png

Calculer les relations Hauteur/Surface/Volume

Dans ce cas, on souhaite calculer les relations surface/volume en fonction de l’altitude de surface libre.

On doit ainsi fournir :

la valeur minimale à considérer
la valeur maximale à considérer
le nombre d’intervalles à calculer
la méthode de calcul

Sur cette base, le code va itérer sur les hauteurs d’eau successives. Il va évaluer les grandeurs utiles (surface et volume) et tracer les courbes résultantes.

Les valeurs sont sauvegardées dans un fichier texte qui est par défaut dans le sous-répertoire “surface_volume” de la matrice chargée.

Est également sauvegardée la matrice contenant les mailles utilisées pour les différents intervalles calculés –> ‘surface_volume_extension.tif’. Attention, la numérotation est basée 1.

ATTENTION : cette approche ne revient pas nécessairement au même résultat que l’intégration des hauteurs d’eau seule. On va travailler ici sur base de l’altitude de surface libre croissante MAIS intégrer les hauteurs d’eau.

[15]:

fig, axs = wel.surface_volume_estimation_from_elevation(desired_zmin= 171, # minimum elevation
                                                        desired_zmax= 173, # maximum elevation
                                                       nb = 50,             # number of steps
                                                       method= 'all below',
                                                       array_to_integrate = wd,
                                                       dirout = Path(wd.filename).parent / 'surface_volume') # array to integrate (water depth)
fig.set_size_inches(10, 4)
fig.tight_layout()

100%|██████████| 51/51 [00:00<00:00, 312.99it/s]

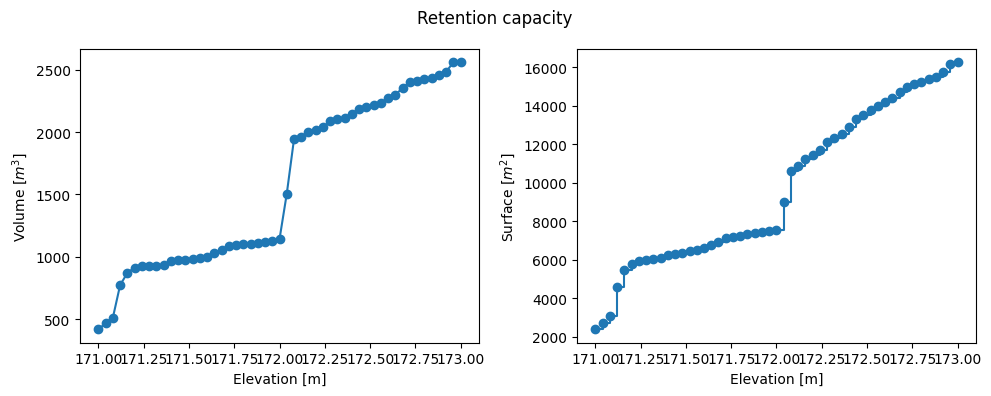
../_images/tutorials_wolfarray_surfacevolume_wel_5_1.png

Récupérer les extensions

[16]:

ext = WolfArray(Path(wd.filename).parent / 'surface_volume' / 'surface_volume_extension.tif')
ext.plot_matplotlib(with_legend=True,)

[16]:

(<Figure size 640x480 with 2 Axes>, <Axes: >)

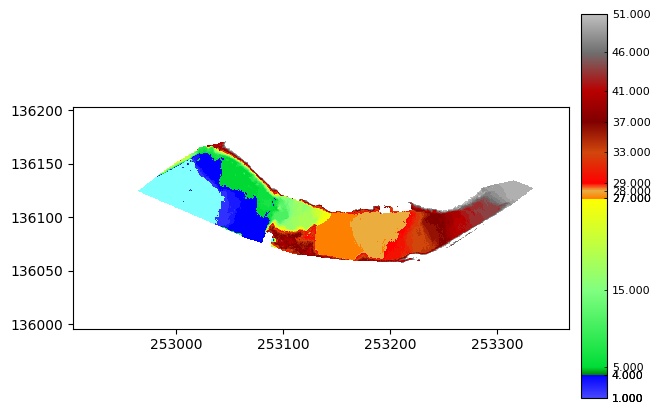
../_images/tutorials_wolfarray_surfacevolume_wel_7_1.png

Et les autres méthodes ?

Il est tout à fait possible de combiner cette approche de calcul avec les autres méthodes de sélection :

‘all below’ : exploite toutes les mailles sous l’altitude courante
‘largest area’ : commence par labelliser la matrice et ne conserve que la plus grande étendue
‘selected’ : commence par labelliser la matrice et ne conserve que la/les zone(s) qui contiennent les coordonnées fournies

Cf le 1er notebook sur cette thématique