Exemple de modélisation d’ouvrages
Potentiellement en charge et avec surverse (type pont - ponceau)
[2]:
from wolfhece.mesh2d.simple_2d import lake_at_rest, water_line, water_lines, unsteady_without_bedmotion, unteaady_with_bedmotion
Vérification du lac au repos
Pour un lac au repos, la surface libre/pression est identique en toute maille.
Le code ne peut en aucun cas mettre l’eau en mouvement, même en présence du pont. Une mise en mouvement indiquerait un mauvais traitement des termes sources de réaction de fond et/ou de toit.
Ici le fond est horizontal pour simplifier les calculs et ne tester que le toit.
3x2 calculs sont effectués: - 1 sans pont - 1 avec pont - pour 3 hauteurs d’eau différentes
Des tests internes sont effectués pour vérifier la cohérence des résultats.
Le calcul n’est pas démarré immédiatement car certaines routines sont compilées à la première exécution (JIT Numba).
[ ]:
fig, axes = lake_at_rest()
0%| | 0.06385508568141009/14400 [00:03<213:43:26, 53.43s/it]
Total time : 0.06385508568141009
Residual : 0.0
0%| | 0.06385508568141009/14400 [00:02<136:30:21, 34.13s/it]
Total time : 0.06385508568141009
Residual : 3.4028825454198546e-16
0%| | 0.05213745913371834/14400 [00:00<?, ?it/s]
Total time : 0.05213745913371834
Residual : 0.0
0%| | 0.05711372491708258/14400 [00:00<08:23, 28.62it/s]
Total time : 0.05711372491708258
Residual : 4.058174235203366e-16
0%| | 0.04515236409857309/14400 [00:00<?, ?it/s]
Total time : 0.04515236409857309
Residual : 0.0
0%| | 0.05213745913371834/14400 [00:00<?, ?it/s]
Total time : 0.05213745913371834
Residual : 3.704589284845265e-16
(<Figure size 1500x1000 with 3 Axes>,
array([<AxesSubplot: >, <AxesSubplot: >, <AxesSubplot: >], dtype=object))
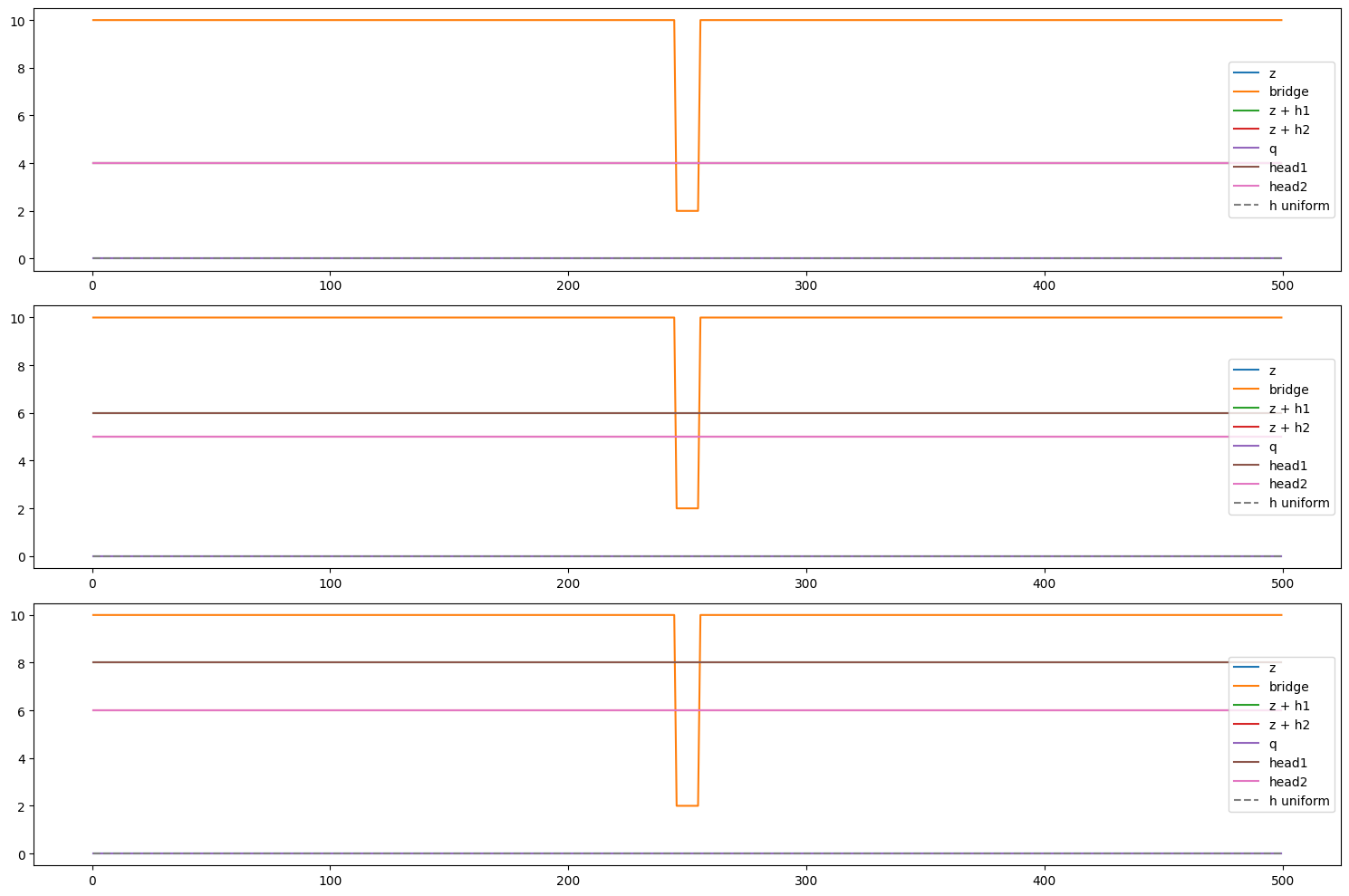
Ligne d’eau
Calcul de lignes d’eau : - sans pont - avec pont
Débit de 7 m²/s ; 3 hauteurs d’eau différentes en condition limite aval.
Il est attendu que la mise en charge augmente avec la hauteur d’eau étant donné que la réaction de toit est plus importante (contraction et élargissement brusque).
La charge est évaluée au centre de la maille. Ceci est une approximation étant donné que cela ne tient pas compte du schéma numérique. Il est donc attendu que la charge sur la dernière maille à surface libre présente un léger pic.
[ ]:
fig, axes = water_line()
24%|██▎ | 3417.451250213751/14400 [00:07<00:24, 446.24it/s]
Total time : 3417.451250213751
Residual : 9.823253321883385e-13
12%|█▏ | 1663.5841980173673/14400 [00:17<02:12, 96.04it/s]
Total time : 1663.5841980173673
Residual : 9.986212834434127e-08
30%|██▉ | 4298.988586931498/14400 [00:05<00:13, 754.78it/s]
Total time : 4298.988586931498
Residual : 9.9298347322474e-13
13%|█▎ | 1871.5112769334007/14400 [00:17<01:59, 104.74it/s]
Total time : 1871.5112769334007
Residual : 9.869046913024704e-08
35%|███▌ | 5073.704821249482/14400 [00:07<00:13, 715.93it/s]
Total time : 5073.704821249482
Residual : 9.78772618509538e-13
13%|█▎ | 1879.559238367564/14400 [00:19<02:10, 95.68it/s]
Total time : 1879.559238367564
Residual : 9.975527071048873e-08
(<Figure size 2000x1000 with 3 Axes>,
array([<AxesSubplot: >, <AxesSubplot: >, <AxesSubplot: >], dtype=object))
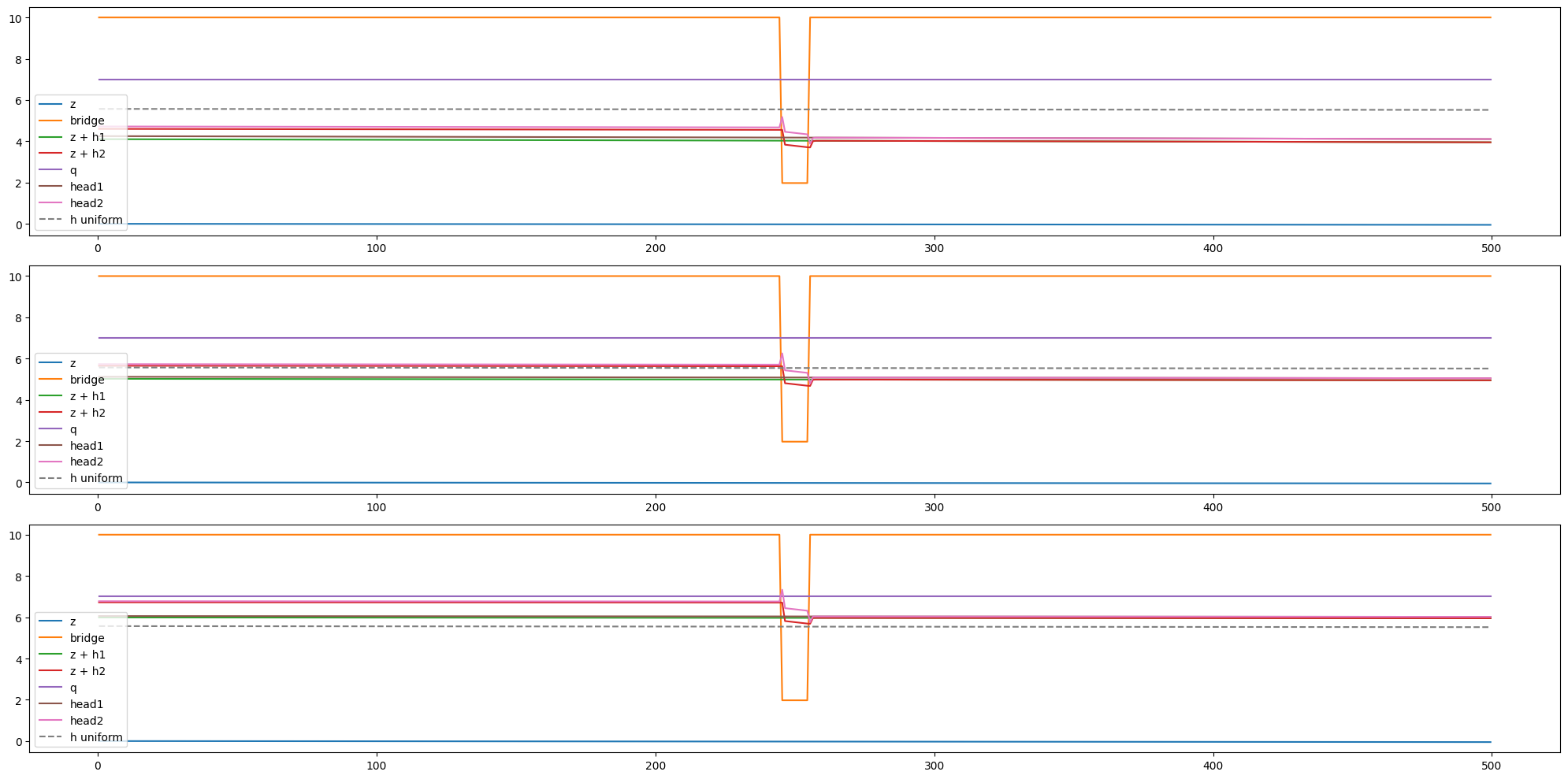
Lignes d’eau et perte de charge
Calcul de plusieurs lignes d’eau et affichage des pertes locales. Comparaison avec les formules de perte de charge par contraction et élargissement brusque.
Contraction :
\[k = 0.5 * \left (1 - \frac {A_{small}}{A_{large}} \right)\]Elargissement :
\[k = \left (1 - \frac {A_{large}}{A_{small}} \right)^2\]
[2]:
fig, axes = water_lines()
17%|█▋ | 2407.222605863859/14400 [00:23<01:58, 101.27it/s]
Total time : 2407.222605863859
Residual : 9.983515125711051e-08
13%|█▎ | 1879.0622572625775/14400 [00:16<01:49, 114.31it/s]
Total time : 1879.0622572625775
Residual : 9.861128980048761e-08
13%|█▎ | 1800.0889064541343/14400 [00:17<01:59, 105.84it/s]
Total time : 1800.0889064541343
Residual : 9.961345970310731e-08
13%|█▎ | 1938.5786658866562/14400 [00:18<02:01, 102.75it/s]
Total time : 1938.5786658866562
Residual : 9.987611448991629e-08
14%|█▍ | 2026.9467943860354/14400 [00:20<02:07, 96.83it/s]
Total time : 2026.9467943860354
Residual : 9.963319946848515e-08
13%|█▎ | 1833.5207359577998/14400 [00:20<02:19, 90.27it/s]
Total time : 1833.5207359577998
Residual : 9.970911918344427e-08
14%|█▍ | 2083.3600667136157/14400 [00:24<02:22, 86.43it/s]
Total time : 2083.3600667136157
Residual : 9.997842553843839e-08
17%|█▋ | 2463.834906706194/14400 [00:30<02:27, 81.15it/s]
Total time : 2463.834906706194
Residual : 9.992566596395136e-08
14%|█▍ | 2059.2803134361056/14400 [00:29<02:58, 69.12it/s]
Total time : 2059.2803134361056
Residual : 9.9805173903178e-08
14%|█▍ | 1993.571221521454/14400 [00:30<03:08, 65.96it/s]
Total time : 1993.571221521454
Residual : 9.950557355864476e-08
13%|█▎ | 1937.8054540924604/14400 [00:31<03:23, 61.16it/s]
Total time : 1937.8054540924604
Residual : 9.952650614764025e-08
[2]:
(<Figure size 2000x1000 with 2 Axes>,
array([<AxesSubplot: >,
<AxesSubplot: xlabel='Computed $\\Delta H$ [m]', ylabel='Theoretical $\\Delta H$ [m]'>],
dtype=object))
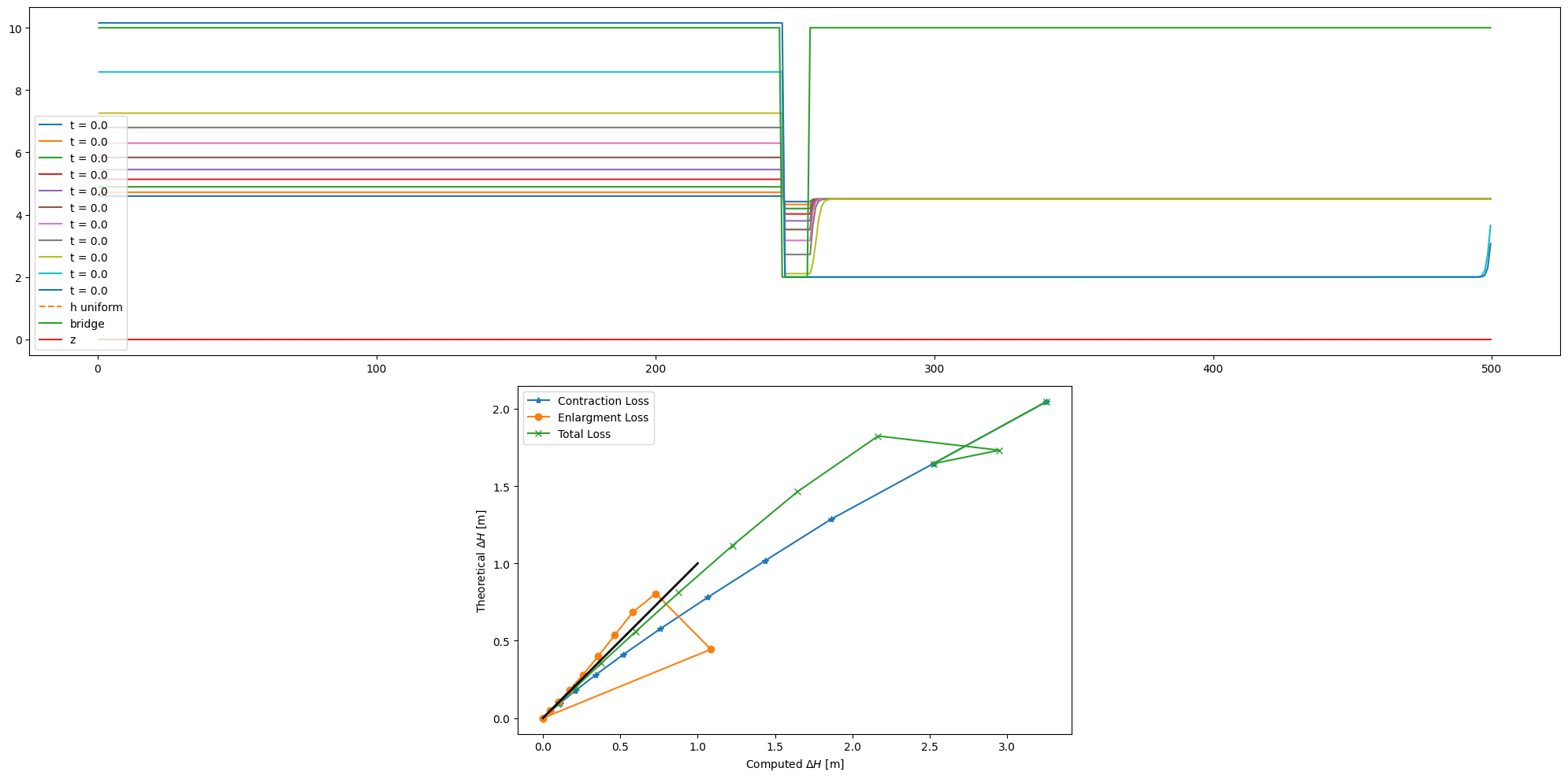
Problème instationnaire
Calcul d’un problème instationnaire avec un débit constant et une conditions limite aval qui évolue.
Extraction des différentes de charge à intervalle régulier et comparaison avec les formules de perte de charge par contraction et élargissement brusque.
[2]:
fig, axes = unsteady_without_bedmotion()
0%| | 0.04704398960516045/14400 [00:03<279:24:37, 69.85s/it]
Total time : 0.04704398960516045
Residual : 0.0
100%|█████████▉| 7189.526609794864/7200 [01:12<00:00, 106.41it/s] d:\ProgrammationGitLab\python3.10\lib\site-packages\tqdm\std.py:533: TqdmWarning: clamping frac to range [0, 1]
full_bar = Bar(frac,
100%|██████████| 7200.004926019133/7200 [01:12<00:00, 98.98it/s]
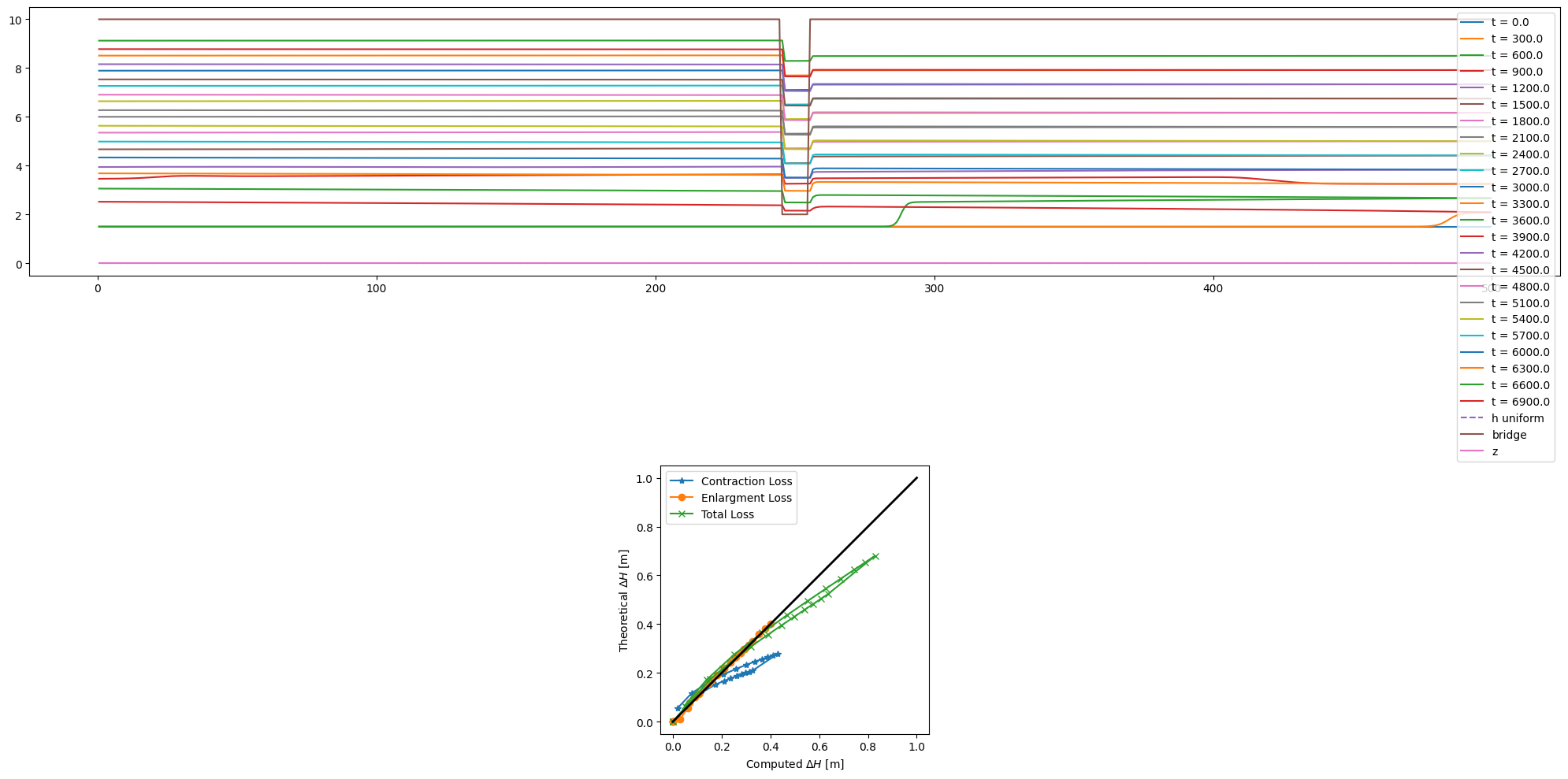
Transitoire avec surverse de l’ouvrage
Modification dynamique de la topographie et du toit.
Problème disponibles :
2 : pont recatngulaire de 20 m de long
6 : pont rectangulaire de 60 m de long
7 : pont triangulaire de 20 m de long
8 : pont en U (poutres latérales plus épaisses) de 20 m de long
9 : ponceau de 100 m de long
Sous-problèmes :
x1 : mouvement de la condition limite aval (mise en charge par l’aval)
x2 : mouvement de la condition limite amont (hydrogramme - mise en charge par dépassement de capacité d’écoulement)
x3 : mouvement de la condition limite amont et de l’aval au moment du pic (mix des 2 premières situations)
[ ]:
# Nécessaire pour l'animation dans le Jupyter Notebook
%matplotlib widget
anim = unteaady_with_bedmotion([81])
ERROR:root:Manning coefficient or slope cannot be null
WARNING:root:Return 99999.
18%|█▊ | 644.0620520671547/3600 [00:05<00:26, 111.71it/s]
Total time : 644.0620520671547
Residual : 9.998784733511457e-08
unsteady_downstream_bc: 100%|██████████| 9002.007815042503/9002.0 [01:31<00:00, 98.69it/s]
[9]:
anim = unteaady_with_bedmotion([82])
ERROR:root:Manning coefficient or slope cannot be null
WARNING:root:Return 99999.
18%|█▊ | 644.0620520671547/3600 [00:05<00:27, 108.92it/s]
Total time : 644.0620520671547
Residual : 9.998784733511457e-08
hydrograph: 100%|██████████| 9002.009025583557/9002.0 [01:29<00:00, 101.08it/s]
[10]:
anim = unteaady_with_bedmotion([83])
ERROR:root:Manning coefficient or slope cannot be null
WARNING:root:Return 99999.
18%|█▊ | 644.0620520671547/3600 [00:06<00:27, 105.95it/s]
Total time : 644.0620520671547
Residual : 9.998784733511457e-08
hydrograph_2steps: 100%|██████████| 9002.053747638016/9002.0 [01:29<00:00, 100.98it/s]